Confidence Interval for the mean

Computes a confidence interval for the mean of the variable (parameter or feature of the process), and prints the data, a histogram with a density line, the result of the Shapiro-Wilks normality test and a quantile-quantile plot.

ss.ci(
  x,
  sigma2 = NA,
  alpha = 0.05,
  data = NA,
  xname = "x",
  approx.z = FALSE,
  main = "Confidence Interval for the Mean",
  digits = 3,
  sub = "",
  ss.col = c("#666666", "#BBBBBB", "#CCCCCC", "#DDDDDD", "#EEEEEE", "#FFFFFF", "#000000",
    "#000000")
)

Arguments

x: A numeric vector with the variable data
sigma2: The population variance, if known
alpha: The eqn\alpha error used to compute the \(100*(1-\\alpha)\%\) confidence interval
data: The data frame containing the vector
xname: The name of the variable to be shown in the graph
approx.z: If TRUE it uses z statistic instead of t when sigma is unknown and sample size is greater than 30. The default is FALSE, change only if you want to compare with results obtained with the old-fashioned method mentioned in some books.
main: The main title for the graph
digits: Significant digits for output
sub: The subtitle for the graph (recommended: six sigma project name)
ss.col: A vector with colors

Value

The confidence Interval.

A graph with the figures, the Shapiro-Wilks test, and a histogram.

Details

When the population variance is known, or the size is greater than 30, it uses z statistic. Otherwise, it is uses t statistic.
If the sample size is lower than 30, a warning is displayed so as to verify normality.

Note

Thanks to the kind comments and suggestions from the anonymous reviewer of a tentative article.

References

Cano, Emilio L., Moguerza, Javier M. and Redchuk, Andres. 2012. Six Sigma with R. Statistical Engineering for Process Improvement, Use R!, vol. 36. Springer, New York. https://link.springer.com/book/10.1007/978-1-4614-3652-2/.

Author

EL Cano

Examples

ss.ci(len, data=ss.data.strings, alpha = 0.05,
  sub = "Guitar Strings Test | String Length", 
  xname = "Length")
#> 	Mean = 950.016; sd = 0.267
#> 	95% Confidence Interval= 949.967 to 950.064
#> 

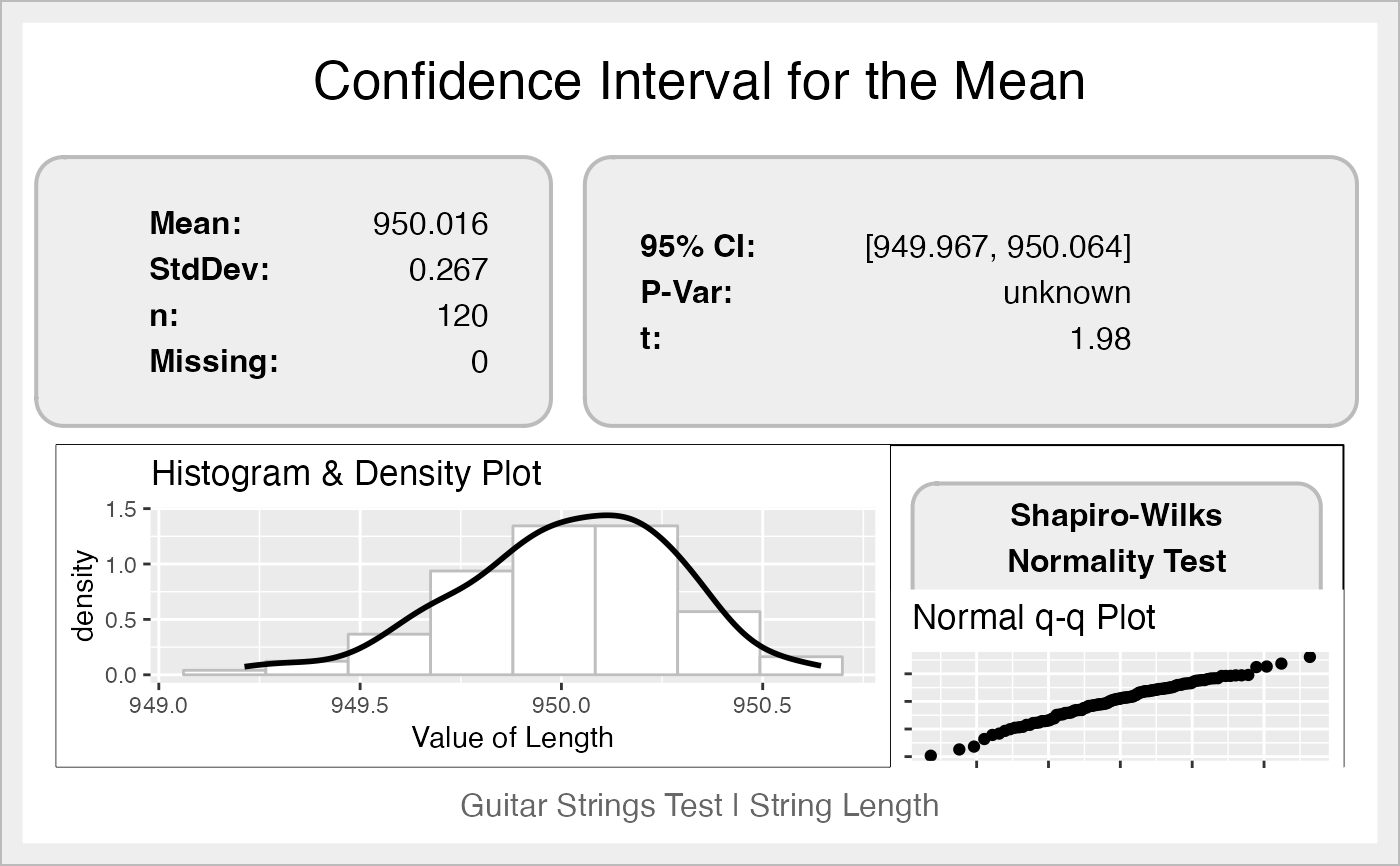#>       LL       UL 
#> 949.9674 950.0640