Capítulo 3 Análisis exploratorio bivariante
3.1 Datos bivariantes y multivariantes
El análisis univariante es muy útil para describir una única característica de la población en estudio. Pero rara vez estudiamos una característica aislada, y lo habitual es tener conjuntos de datos con varias variables (cuantitativas y cualitativas) que podemos estudiar por separado (análisis univariante) o conjuntamente (análisis multivariante).
El caso especial del análisis bivariante es cuando estudiamos dos características a la vez: \(X, Y\). Nos interesa la relación entre ellas, para lo que realizaremos resúmenes numéricos y gráficos. Los datos bivariantes se encontrarán como pares de valores \((x_i, y_i)\) para cada observación \(i = 1, \ldots, n\).
Cuando estudiamos más de dos variables, tenemos datos multivariantes. En este caso, estudiamos las relaciones “dos a dos” entre las variables (como en el caso bivariante) y la estructura conjunta. Hay algunas técnicas multivariantes específicas para este último caso. En este capítulo nos vamos a centrar solo en el primer caso.
3.2 Frecuencias conjuntas, marginales y condicionadas
El primer resumen que podemos hacer de datos bivariante es la tabla de frecuencias conjunta. Igual que en el caso univariante \(n\) es número total de datos, es decir, la frecuencia total. La frecuencia absoluta conjunta, \(n_{ij}\), es el número de observaciones en la clase \(i\) de \(X\) y en la clase \(j\) de \(Y\). La frecuencia relativa conjunta es \(f_{ij}= \frac{n_{ij}}{n}\).
3.2.1 Distribución conjunta de frecuencias
Las frecuencias conjuntas se representan en una tabla de doble entrada, con los valores de una variable en filas y los de la otra en columnas. En el interior, se ponen las frecuencias conjuntas (absolutas, relativas o ambas). Si las dos variables son cualitativas, la tabla se denomina Tabla de contingencia.
La Tabla 3.1 muestra la tabla de contingencia de los analistas y el tipo de queso en el ejemplo del análisis de la producción de quesos. Asignamos la variable \(X\) al Analista (en filas) y la variable \(Y\) al Tipo (en columnas). La Tabla 3.2 muestra la tabla de frecuencias relativas de los mismos datos. El número total de datos es \(n= 1171\).
| A | B | C | |
|---|---|---|---|
| analista_10 | 52 | 47 | 219 |
| analista_13 | 42 | 36 | 198 |
| analista_6 | 44 | 32 | 235 |
| analista_9 | 37 | 33 | 196 |
| A | B | C | |
|---|---|---|---|
| analista_10 | 0.04 | 0.04 | 0.19 |
| analista_13 | 0.04 | 0.03 | 0.17 |
| analista_6 | 0.04 | 0.03 | 0.20 |
| analista_9 | 0.03 | 0.03 | 0.17 |
En el caso de variables continuas, debemos tener los datos agrupados en intervalos (clases).
La tabla 3.3 contiene las frecuencias absolutas conjuntas de las variables:
\(X\) = ph (filas);
\(Y\) = est (columnas)
| (28,30] | (30,32] | (32,34] | (34,36] | (36,38] | |
|---|---|---|---|---|---|
| (6.35,6.4] | 0 | 0 | 1 | 0 | 0 |
| (6.4,6.45] | 0 | 0 | 0 | 0 | 0 |
| (6.45,6.5] | 1 | 2 | 0 | 0 | 0 |
| (6.5,6.55] | 3 | 50 | 1 | 0 | 0 |
| (6.55,6.6] | 17 | 129 | 36 | 2 | 0 |
| (6.6,6.65] | 18 | 195 | 167 | 20 | 4 |
| (6.65,6.7] | 9 | 160 | 182 | 18 | 0 |
| (6.7,6.75] | 2 | 53 | 70 | 4 | 0 |
| (6.75,6.8] | 0 | 9 | 10 | 2 | 0 |
| (6.8,6.85] | 0 | 4 | 1 | 0 | 1 |
3.2.2 Distribución marginal
Si partimos de la distribución conjunta, podemos obtener la de cada una de las variables (marginal) y estudiarla como datos univariantes. Basta con hacer las sumas por filas (para la marginal de \(X\)), o por columnas, (para la marginal de \(Y\)):
- Frecuencias marginales de \(X\):
- Absolutas: \(n_{i\cdot} = \sum\limits_{j = 1}^{n_j}n_{ij}\)
- Relativas: \(f_{i\cdot} = \sum\limits_{j = 1}^{n_j}f_{ij}\)
- Frecuencias marginales de \(Y\):
- \(n_{\cdot j} = \sum\limits_{i = 1}^{n_i}n_{ij}\)
- \(f_{\cdot j} = \sum\limits_{i = 1}^{n_i}f_{ij}\)
donde \(n_i\) es el número de clases de la variable \(X\) y \(n_j\) es el número de clases de la variable \(Y\). Análogamente, para frecuencias marginales relativas sumamos las frecuencias relativas conjuntas, o bien dividimos las frecuencias absolutas marginales entre el número total de datos \(n\).
La tabla 3.4 contiene las frecuencias marginales como suma de filas y columnas de la distribución conjunta en la tabla 3.3. Las distribuciones marginales de \(X\) y de \(Y\) por separado se muestran en las tablas 3.5 y 3.6 respectivamente.
| X\Y | (28,30] | (30,32] | (32,34] | (34,36] | (36,38] | Sum |
|---|---|---|---|---|---|---|
| (6.35,6.4] | 0 | 0 | 1 | 0 | 0 | 1 |
| (6.4,6.45] | 0 | 0 | 0 | 0 | 0 | 0 |
| (6.45,6.5] | 1 | 2 | 0 | 0 | 0 | 3 |
| (6.5,6.55] | 3 | 50 | 1 | 0 | 0 | 54 |
| (6.55,6.6] | 17 | 129 | 36 | 2 | 0 | 184 |
| (6.6,6.65] | 18 | 195 | 167 | 20 | 4 | 404 |
| (6.65,6.7] | 9 | 160 | 182 | 18 | 0 | 369 |
| (6.7,6.75] | 2 | 53 | 70 | 4 | 0 | 129 |
| (6.75,6.8] | 0 | 9 | 10 | 2 | 0 | 21 |
| (6.8,6.85] | 0 | 4 | 1 | 0 | 1 | 6 |
| Sum | 50 | 602 | 468 | 46 | 5 | 1171 |
| \(x_i\) | \(n_{i·}\) | \(f_{i·}\) |
|---|---|---|
| (6.35,6.4] | 1 | 0.001 |
| (6.4,6.45] | 0 | 0.000 |
| (6.45,6.5] | 3 | 0.003 |
| (6.5,6.55] | 54 | 0.046 |
| (6.55,6.6] | 184 | 0.157 |
| (6.6,6.65] | 404 | 0.345 |
| (6.65,6.7] | 369 | 0.315 |
| (6.7,6.75] | 129 | 0.110 |
| (6.75,6.8] | 21 | 0.018 |
| (6.8,6.85] | 6 | 0.005 |
| Sum | 1171 | 1.000 |
| \(y_j\) | \(n_{·j}\) | \(f_{·j}\) |
|---|---|---|
| (28,30] | 50 | 0.043 |
| (30,32] | 602 | 0.514 |
| (32,34] | 468 | 0.400 |
| (34,36] | 46 | 0.039 |
| (36,38] | 5 | 0.004 |
| Sum | 1171 | 1.000 |
3.2.3 Distribución condicionada
La distribución de la variable \(Y\) condicionada a un valor \(x_i\) de la variable \(X\) se representa por \(Y | X = x_i\). Análogamente se puede definir para varios valores de \(X\), o de \(X\) condicionada a \(Y\). Se lee “Distribución de \(Y\) condicionada a que \(X\) es igual a \(x_i\)”. Estas distribuciones condicionadas son variables univariantes que se pueden estudiar con análisis univariante.
A partir de la distribución conjunta, tomaríamos la fila o columna que se corresponde con el valor “conocido”, es decir, el de la condición. Las frecuencias relativas se calcularán dividiendo entre la frecuencia marginal, y no entre la frecuencia total. Por ejemplo:
\[ f_{x_i|y=y_j}=\frac{n_{ij}}{n_{·j}}. \]
La tabla 3.7 muestra la distribución De \(X\) condicionada a que \(Y = y_2\). Es decir, como es una variable numérica que hemos dividido en intervalos, condicionada a que \(Y \in (30,32]\). La tabla 3.8 muestra la distribución de \(Y\) condicionada a que \(X = x_5\), es decir, de \(Y | X \in (6.55,6.6]\).
| \(x_i\) | \(n_{i|j=2}\) | \(f_{i|j=2}\) |
|---|---|---|
| (6.35,6.4] | 0 | 0.000 |
| (6.4,6.45] | 0 | 0.000 |
| (6.45,6.5] | 2 | 0.003 |
| (6.5,6.55] | 50 | 0.083 |
| (6.55,6.6] | 129 | 0.214 |
| (6.6,6.65] | 195 | 0.324 |
| (6.65,6.7] | 160 | 0.266 |
| (6.7,6.75] | 53 | 0.088 |
| (6.75,6.8] | 9 | 0.015 |
| (6.8,6.85] | 4 | 0.007 |
| Sum | 602 | 1.000 |
| \(y_{j}\) | \(n_{j|i=5}\) | \(f_{j|i=5}\) |
|---|---|---|
| (28,30] | 17 | 0.092 |
| (30,32] | 129 | 0.701 |
| (32,34] | 36 | 0.196 |
| (34,36] | 2 | 0.011 |
| (36,38] | 0 | 0.000 |
| Sum | 184 | 1.000 |
3.2.4 Independencia de variables
Cuando la distribución de una variable \(X\) no varía en función de los valores de otra variable \(Y\), entonces las variables \(X\) e \(Y\) son estadísticamente independientes. Equivalentemente, la distribución de \(X | Y=y_j\) es igual para cualquier valor de \(y_j\). Es decir, si son independientes se cumple:
\[ f_{ij} = f_{i.}\cdot f_{.j} \;\forall i, j. \]
La tabla ?? muestra la distribución conjunta y marginales de las variables discretizadas pH y Extracto Seco Total. Para que fueran independientes, todos los productos \(f_{i.}\cdot f_{.j}\) deberían ser iguales a \(f_{ij}\), es decir, la distribución de \(X\) no debería variar en función de los valores de \(Y\), y viceversa. En este caso, se puede ver que no se cumple esta igualdad (por ejemplo $0,043 != 0), por lo que las variables no son independientes.
| (28,30] | (30,32] | (32,34] | (34,36] | (36,38] | Sum | |
|---|---|---|---|---|---|---|
| (6.35,6.4] | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.001 |
| (6.4,6.45] | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| (6.45,6.5] | 0.001 | 0.002 | 0.000 | 0.000 | 0.000 | 0.003 |
| (6.5,6.55] | 0.003 | 0.043 | 0.001 | 0.000 | 0.000 | 0.046 |
| (6.55,6.6] | 0.015 | 0.110 | 0.031 | 0.002 | 0.000 | 0.157 |
| (6.6,6.65] | 0.015 | 0.167 | 0.143 | 0.017 | 0.003 | 0.345 |
| (6.65,6.7] | 0.008 | 0.137 | 0.155 | 0.015 | 0.000 | 0.315 |
| (6.7,6.75] | 0.002 | 0.045 | 0.060 | 0.003 | 0.000 | 0.110 |
| (6.75,6.8] | 0.000 | 0.008 | 0.009 | 0.002 | 0.000 | 0.018 |
| (6.8,6.85] | 0.000 | 0.003 | 0.001 | 0.000 | 0.001 | 0.005 |
| Sum | 0.043 | 0.514 | 0.400 | 0.039 | 0.004 | 1.000 |
3.3 Representación gráfica conjunta
3.3.1 Gráficos de barras
Al igual que en el caso univariante, la mejor representación de tablas de frecuencias para variables cualitativas y para variables numéricas discretas sigue siendo el gráfico de barras. Hay varias variantes para representar las dos variables:
El eje horizontal del gráfico representa las clases de ambas variables \(X\) e \(Y\) de las variables, y se representan barras que representan las frecuencias absolutas conjuntas.
El eje horizontal del gráfico representa las clases de una de las variables, la altura total de las barras representa la frecuencia absoluta de esa variable, y cada barra se divide en trozos cuya altura es la frecuencia absoluta conjunta.
El eje horizontal del gráfico representa las clases de una de las variables, la altura total de las barras representa el 100% (todas la misma altura), y cada barra se divide en trozos cuya altura es la frecuencia relativa condicionada a la clase de la barra.
La figura 3.1 muestra la representación de la tabla de frecuencias 3.1 con las barras adyacentes, mientras que la figura 3.2 la representa con las barras apiladas. La figura 3.3 muestra la representación de la tabla de frecuencias de la variable “analista” condicionadas a cada tipo de queso.
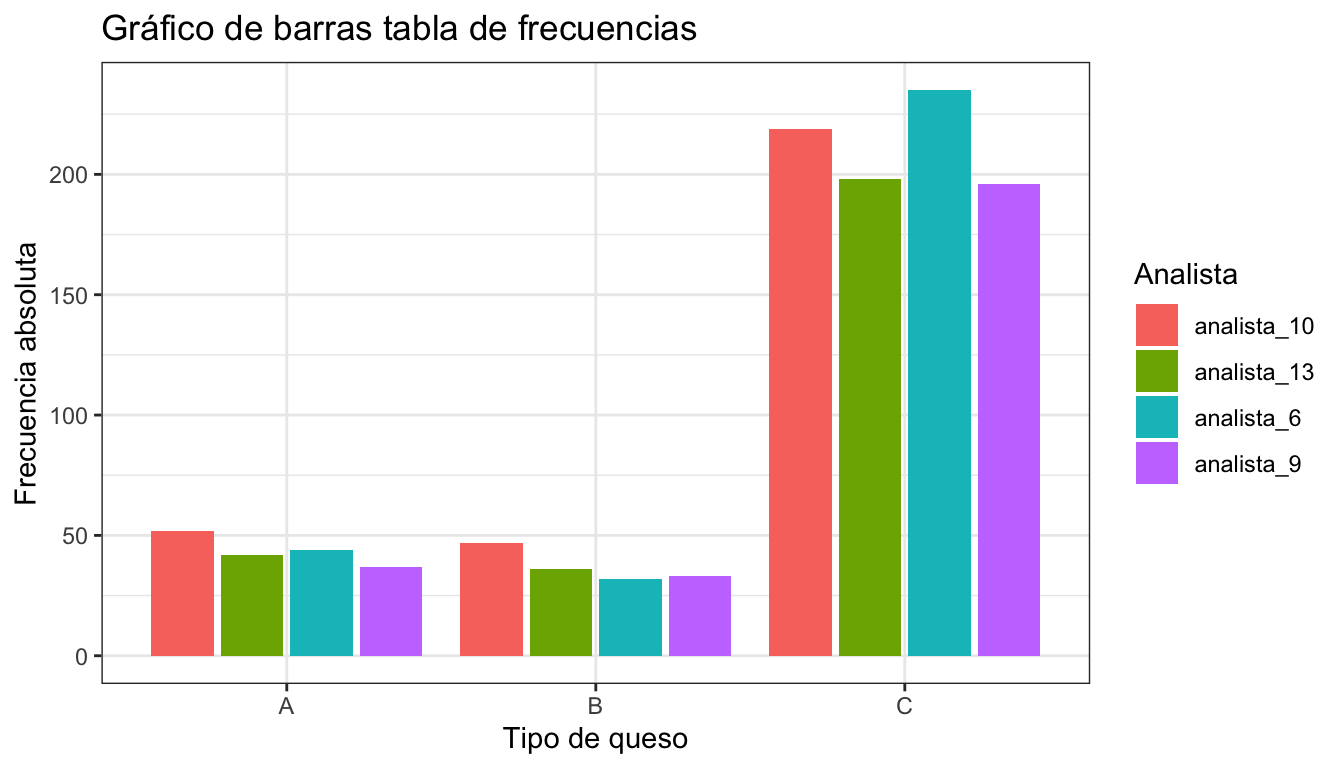
Figura 3.1: Gráfico de barras con frecuencias conjuntas
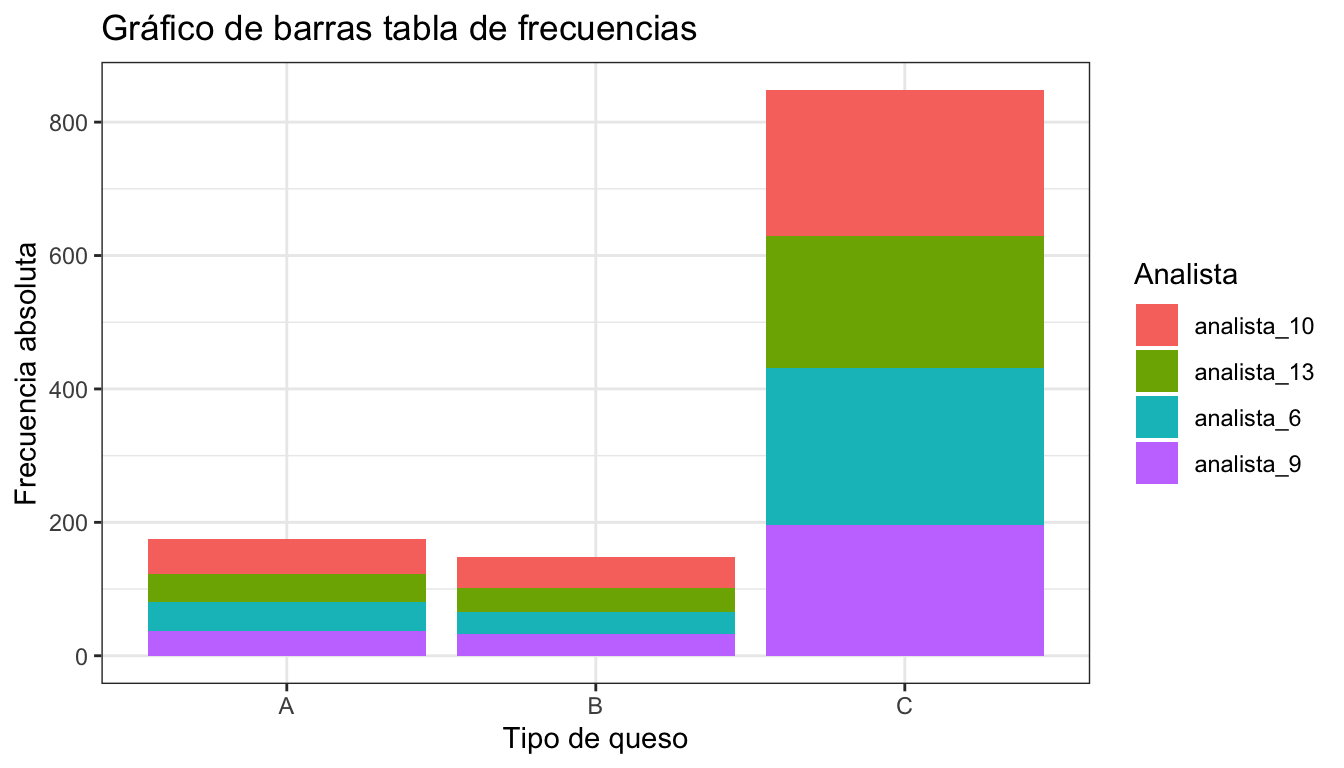
Figura 3.2: Gráfico de barras con frecuencias conjuntas apiladas
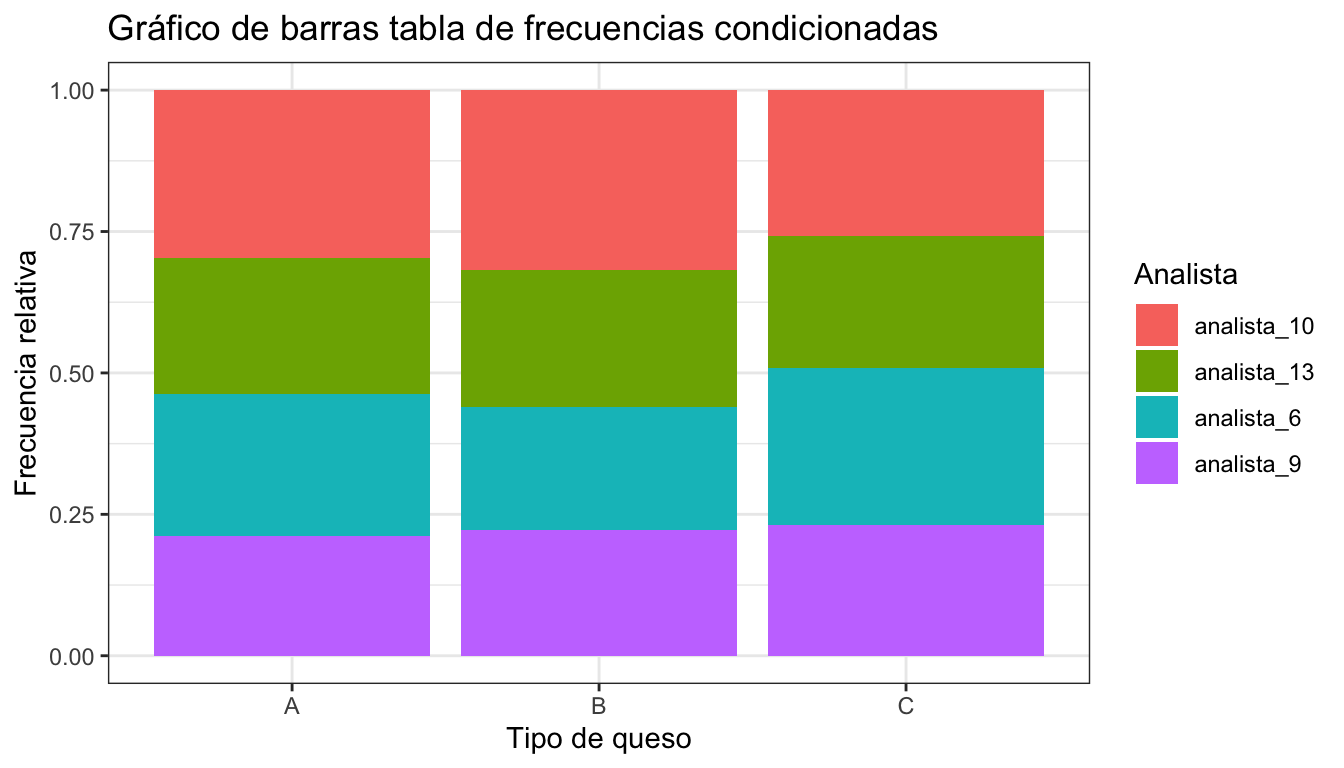
Figura 3.3: Gráfico de barras con frecuencias condicionadas
Los gráficos de sectores son una representación muy popular para representar tablas de frecuencias, aunque en general no están recomendados ya que el ojo humano no es muy bueno para apreciar las diferencias entre ángulos, en comparación con la capacidad para distinguir alturas.
Las tablas de frecuencias conjuntas de variables continuas agrupadas en intervalos se pueden representar también mediante gráficos de barras igual que las cualitativas y las discretas. No obstante, si disponemos de todos los datos, es más adecuado utilizar las representaciones que se explican a continuación.
3.3.2 El gráfico de dispersión
Para dos variables continuas, la representación más adecuada es el gráfico de dispersión. El gráfico de dispersión es una “nube de puntos” representada en unos ejes cartesianos \(X\), \(Y\), que representan las escalas de cada una de las variables. Cada punto representa un par de valores \((x_i, y_i)\). Este gráfico permite apreciar a simple vista si hay relación lineal o de otro tipo entre ambas variables.
La figura 3.4 representa la variable “est” (extracto seco total) frente al pH en el ejemplo de los quesos. Se ha añadido transparencia a los puntos para apreciar dónde hay mayor densidad de datos. A simple vista no se ve una relación clara. Si añadimos algunos elementos al gráfico, podemos descubrir algo más. El gráfico de la izquierda de la figura 3.5 añade una línea de tendencia suavizada en la que parece que hay un intervalo del pH en el que el est crece en la misma dirección (entre 6,5 y 6,6 aproximadamente). En el gráfico de la derecha de la misma figura 3.5 hemos añadido una “capa” de color representando el tipo de queso. Aquí se puede ver claramente como la “masa” inferior de puntos se corresponde con quesos distintos a los de la “masa” superior.
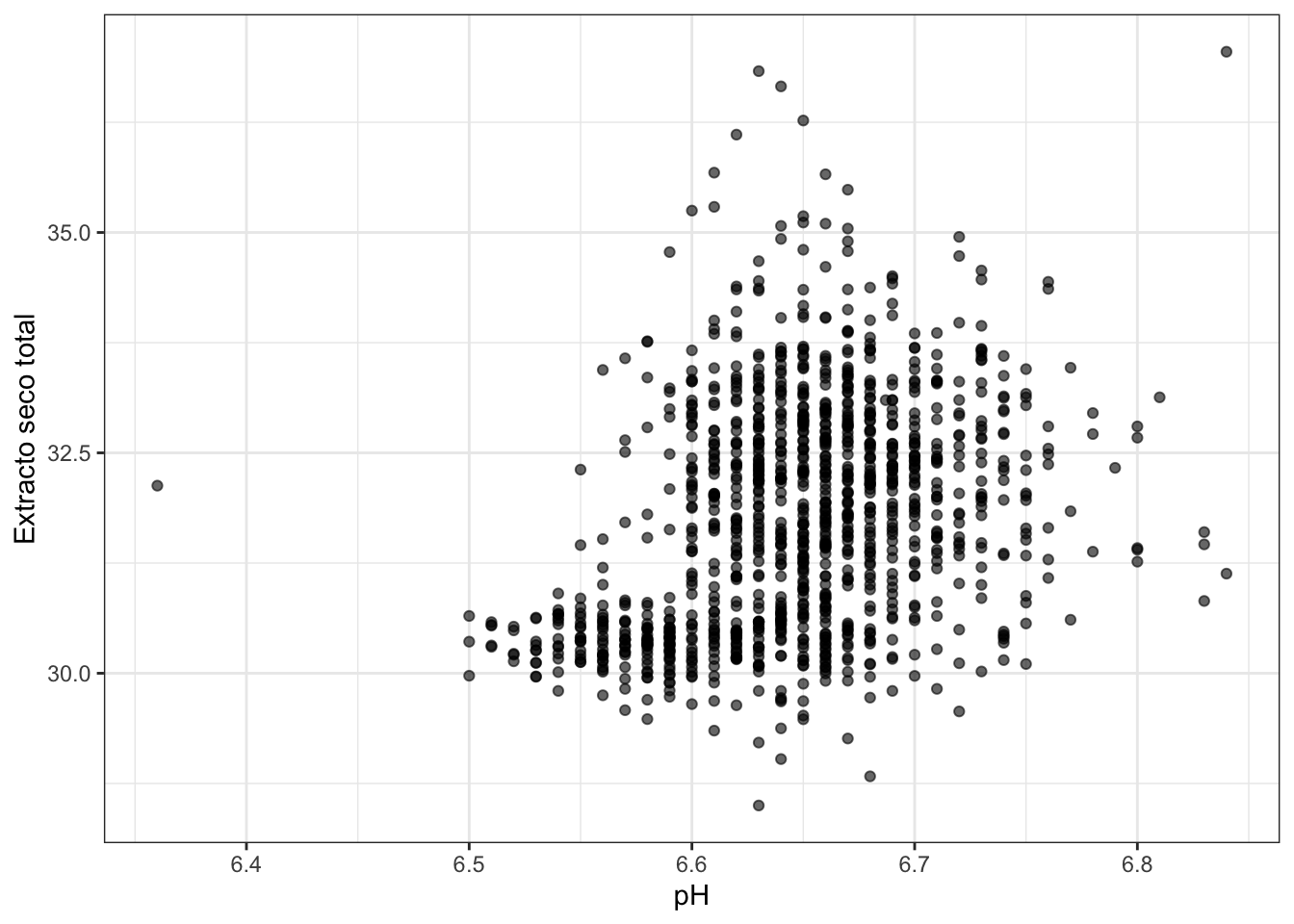
Figura 3.4: Gráfico de dispersión del ejemplo de los quesos
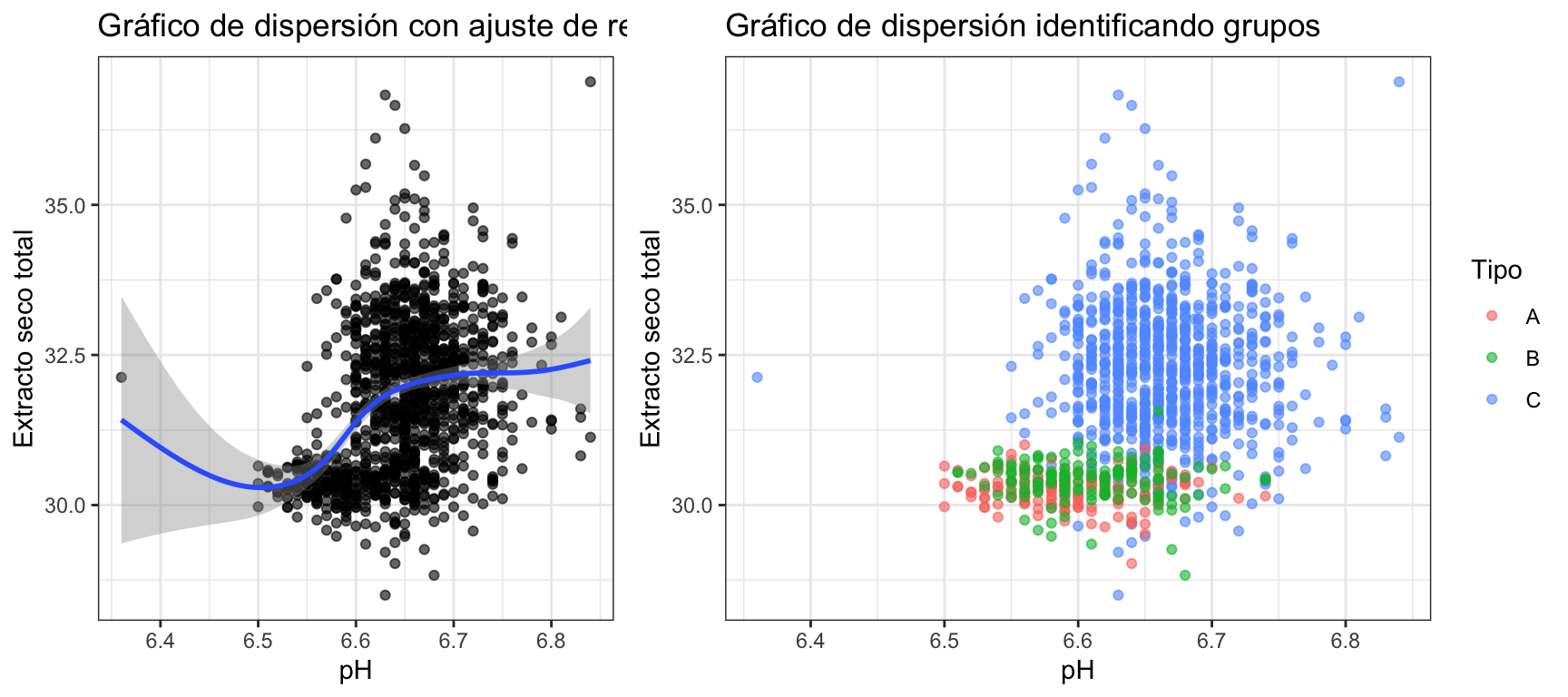
Figura 3.5: Gráficos de dispersión ‘enriquecidos’
3.3.3 Gráficos de cajas por grupos
Cuando queremos estudiar conjuntamente una variable cuantitativa y una variable cualitativa, la representación más adecuada es mediante gráficos de cajas representando en el eje horizontal las clases de la variable cualitativa. De esta forma podemos comparar los principales estadísticos en cada uno de los grupos. Los gráficos de cajas pueden ocultar información importante acerca de la distribución, por lo que otra representación muy útil es el gráfico de densidad por grupos. También se pueden añadir capas de puntos, o utilizar el gráfico de violín que suaviza la caja a la forma de la distribución.
En la figura 3.6 se representa la relación entre el tipo de queso y el pH. El gráfico de la izquierda muestra el gráficos de cajas, y el de la derecha, un gráfico de violín. La figura 3.7 mustra gráficos de densidad de la variable pH para cada tipo de queso. En ambos casos se aprecia claramente el comportamiento diferente de los quesos de tipo C.
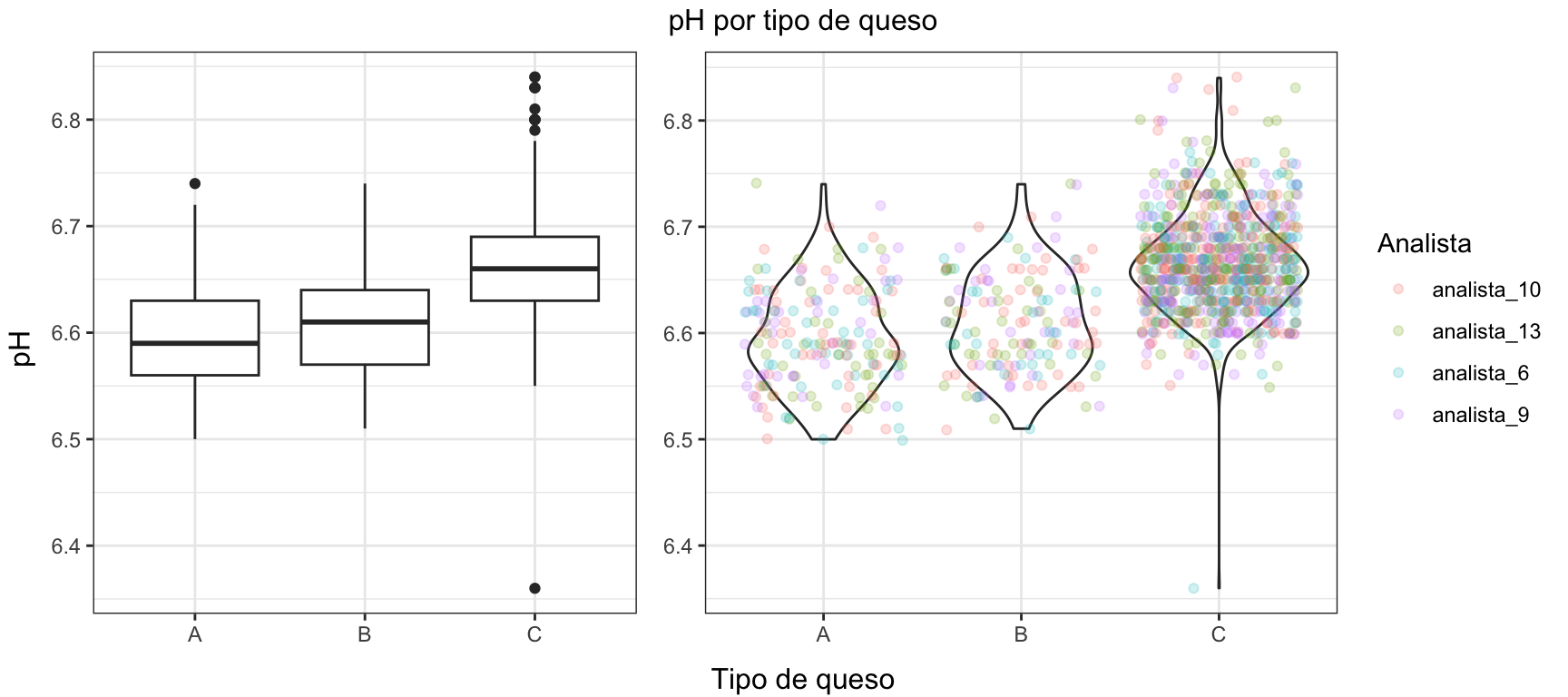
Figura 3.6: Representación de la relación entre pH y tipo de queso
lab |>
ggplot(aes(x = ph, colour = tipo, fill = tipo)) +
geom_density(alpha = 0.4) +
theme_bw() +
labs(title = "Gráficos de densidad por tipo de queso",
x = "pH",
y = "Densidad",
fill = "Tipo de queso",
colour = "Tipo de queso") 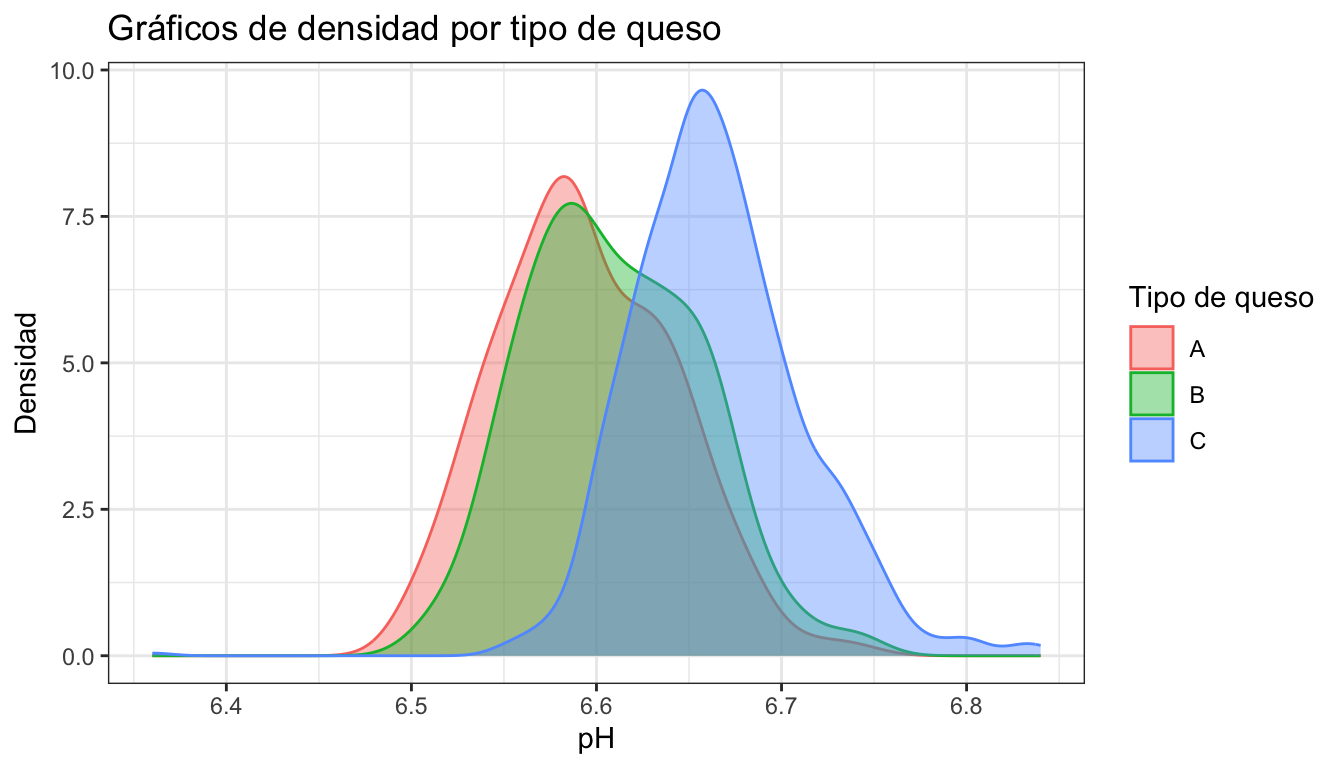
Figura 3.7: Gráficos de densidad por grupos
3.4 Medidas conjuntas
Al igual que en el caso univariante, podemos obtener medidas conjuntas de dos variables que resuman su relación.
3.4.1 Covarianza
La medida más importante es la covarianza. La covarianza mide la dependencia lineal entre las variables, y se define como:
\[ \sigma_{xy} = \frac{1}{N} \sum\limits_{i=1}^N(X_i-\bar X)(Y_i-\bar Y) \]
Para datos muestrales, dividimos por \(n - 1\):
\[ s_{xy} = \frac{1}{n-1} \sum\limits_{i=1}^n(x_i-\bar x)(y_i-\bar y) \]
- Si \(s_{xy} > 0\): Relación lineal positiva (cuando una crece, la otra también).
- Si \(s_{xy} < 0\): Relación lineal negativa (cuando una crece, la otra decrece).
- Si \(s_{xy} = 0\): No hay relación lineal.
Decimos que hay relación lineal cuando una variable se puede expresar en función de la otra como una transformación lineal, es decir: \(Y=a+bX\). Esta sería una relación perfecta entre dos variables. En la práctica, habrá cierto “error” en esta relación, como veremos más adelante.
Podemos realizar el cálculo abreviado al igual que con la varianza. Según el caso:
- Covarianza poblacional con todos los datos:
\[ \sigma_{xy} = \frac{1}{N} \sum\limits_{i=1}^N(X_i \cdot Y_i) - \bar X \cdot \bar Y. \]
- Covarianza poblacional con tablas de frecuencias:
\[ \sigma_{xy} = \frac{1}{N} \sum\limits_{i=1}^N(n_i \cdot X_i \cdot Y_i) - \bar X \cdot \bar Y. \]
- Covarianza muestral, con todos los datos:
\[ s_{xy} = \frac{1}{n-1} \left ( \sum\limits_{i=1}^n(x_i \cdot y_i) - n \cdot \bar x \cdot \bar y \right ). \]
Una propiedad importante de la covarianza es que si \(X\) e \(Y\) son variables independientes, su covarianza es cero. Lo contrario no tiene por qué ser verdad, ya que puede existir una relación no lineal, como veremos más adelante.
La covarianza es un estadístico muy importante para aplicar muchas técnicas estadísticas. Sin embargo, su interpretación más allá del signo no es muy útil, ya que no está acotada: depende de las unidades de las variables.
3.4.2 Correlación
Para interpretar la relación lineal entre dos variables, en vez de la covarianza calcularemos el coeficiente de correlación lineal, que sí está acotado, en concreto entre -1 y 1:
\[ r_{xy}=\frac{s_{xy}}{s_x \cdot s_y}. \]
- Si \(r_{xy}\) próximo a 0, no hay relación lineal
- Si \(r_{xy}\) próximo a -1 o 1, relación lineal fuerte, negativa o positiva respectivamente
- Si \(|r_{xy}| = 1\) relación lineal perfecta. Aparece también al correlacionar una variable con sí misma.
Un conjunto de datos bivariantes quedará caracterizado por su vector de medias y su matriz de varianzas-covarianzas. El vector de medias contiene las medias de las dos variables:
\[ \left [ \begin{array}{c}\bar x\\ \bar y\end{array}\right ]. \]
La Matriz de varianzas-covarianzas, o simplemente matriz de covarianzas, sería:
\[ \mathbf{S} = \left [\begin{array}{cc} s^2_x & s_{xy}\\ s_{xy} & s_y^2 \end{array}\right ] \]
Mientras que la matriz de correlaciones tendría valores igual a 1 en la diagonal, y el coeficiente de correlación fuera de la diagonal:
\[ \mathbf{R} = \left [\begin{array}{cc} 1 & r_{xy}\\ r_{xy} & 1 \end{array}\right ] \]
En el ejemplo de la producción de quesos, si tomamos \(X\) = ph; \(Y\) = est, tenemos los siguientes datos resumidos:
\[ n = 1.171;\; \sum x_i = 7.784,447;\; \sum y_i = 37.203,32 \]
\[ \sum x_i^2 = 51.752,12;\; \sum y_i^2 = 1.183.966 ;\; \sum x_i y_i = 247.344,4 \]
el vector de medias sería:
\[ \left [ \begin{array}{c} 6,648\\ 31,771\end{array}\right ],\]
y la matriz de covarianzas (muestrales)
\[\mathbf{S} = \left [\begin{array}{cc} s^2_x & s_{xy}\\ s_{xy} & s_y^2 \end{array}\right ]=\left [\begin{array}{cc} 0,003 & 0,0241\\ 0,0241 & 1,7061 \end{array}\right ] \]
El coeficiente de correlación lineal será entonces:
\[ r_{xy}=\frac{s_{xy}}{s_x \cdot s_y}= \frac{0,0241}{\sqrt{0,003\cdot 1,7061}} = 0,3366. \]
3.4.3 Caso multivariante
En el caso de estudiar más de dos características numéricas, se extiende la matriz de covarianzas a cualquier número de variables. En este caso las matrices de covarianzas y de correlaciones tendrán tantas filas o columnas como variables. Estas matrices se utilizan en cálculo multivariante y multitud de métodos estadísticdos. Una propiedad importante de la matriz de covarianzas es que si previamente tipificamos las variables, la matriz de covarianzas de la variable tipificada es igual a la matriz de correlaciones de las variables originales.
Con el código a continuación obtenemos la matriz de correlaciones de todas las variables numéricas del conjunto de datos de la producción de queso.
lab |> select(where(is.numeric), -codigo) |>
drop_na() |>
cor() |>
round(2)
est mg sal ph bacteriax
est 1.00 -0.27 0.62 0.37 0.01
mg -0.27 1.00 -0.49 -0.44 -0.01
sal 0.62 -0.49 1.00 0.46 0.00
ph 0.37 -0.44 0.46 1.00 -0.12
bacteriax 0.01 -0.01 0.00 -0.12 1.00
imperfecciones -0.03 0.00 0.00 0.03 -0.02
imperfecciones
est -0.03
mg 0.00
sal 0.00
ph 0.03
bacteriax -0.02
imperfecciones 1.003.4.4 Patrones en los gráficos
La nube de puntos del gráfico de dispersión nos da una idea de la relación entre las variables. También nos da pistas de cómo será el coeficiente de correlación. Es importante volver a resaltar que Los resúmenes numéricos pueden estar escondiendo información importante, por ejemplo relaciones no lineales. La figura 3.8 muestra los gráficos de dispersión de dos variables y sus correspondientes coeficientes de correlación. Los dos primeros gráficos de la primera columna muestran una relación perfecta, mientras que el tercero muestra ausencia de correlación, y además independencia (no se aprecia otro tipo de relación, solo “ruido”). En la segunda columna, el primer gráfico muestra una alta correlación lineal, es decir hay una relación fuerte entre las variables. El segundo sin embargo también muestra relación lineal, pero más moderada. El último gráfico ilustra cómo una correlación muy baja, próxima a cero, indica que no hay relación lineal, como en el gráfico de la izquierda. Si embargo, no podemos decir que las variables sean independientes, porque hay claramente una dependencia funcional entre la \(X\) y la \(Y\), pero no es lineal.
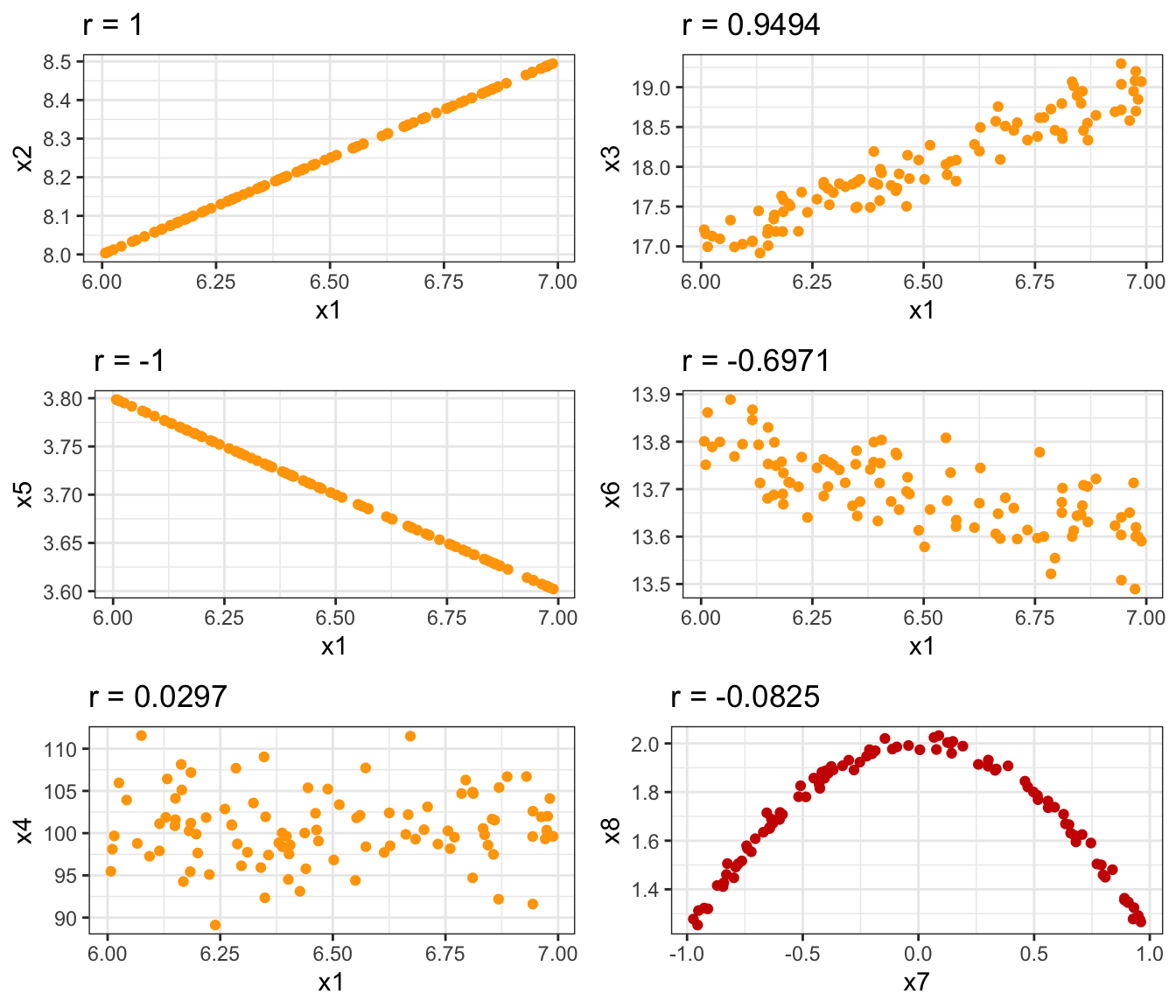
Figura 3.8: Patrones en la nube de puntos según el coeficiente de correlación
3.5 Regresión lineal simple
Las técnicas de regresión, de manera general tratan de encontrar una relación funcional entre una variable dependiente \(Y\) y una o más variables independientes \(X\):
\[ Y = f(\mathbf{X}) + \varepsilon. \]
En el caso más sencillo de una sola variable independiente, cuando existe relación lineal los puntos del gráfico de dispersión se disponen alrededor de una línea recta, y podemos expresar la relación mediante la ecuación de la recta que mejor se aproxima a la nube de puntos. Esta aproximación estará ligada a un error, representado en la expresión anterior por \(\varepsilon\), que mediremos con la variabilidad alrededor de la línea, de forma análoga a como la varianza expresa la variabilidad de los datos entorno a la media. Así, la recta de regresión quedaría expresada como:
\[ Y = a + bX + \varepsilon, \]
donde \(X\) es la variable independiente o explicativa, \(Y\) es la variable dependiente o variable respuesta, \(a\) y \(b\) son los coeficientes de regresión (término independiente y pendiente de la recta respectivamente) y \(\varepsilon\) es el error.
3.5.1 Estimación de los coeficienetes
Tenemos pares de datos \((x_i, y_i)\) que queremos ajustar al modelo matemático de la recta. Para cualesquiera valores de \(a\) y \(b\) que elijamos, podemos aproximar los valores de \(y_i\) como:
\[ \hat{y}_i = a + bx_i. \]
Esta aproximación tiene un error, que es el residuo de esa observación:
\[ y_i = \hat y + \varepsilon_i \implies \varepsilon_i=y_i - \hat{y}_i. \]
La figura 3.9 esquematiza la relación entre los valores de la variable bivariante (puntos naranjas), la recta de regresión (línea azul) y los residuos (líneas negras).
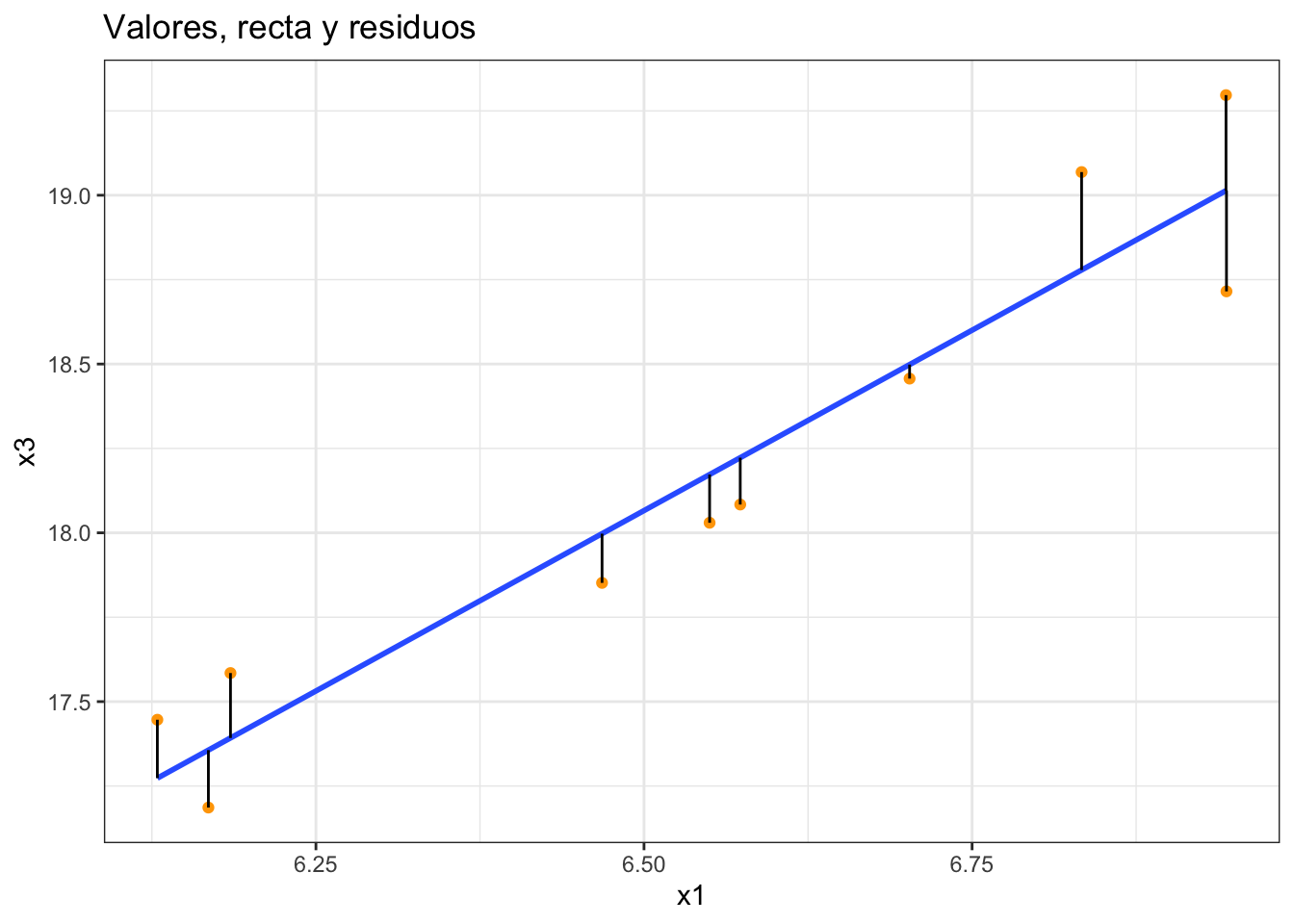
Figura 3.9: Esquematización de los valores, recta y residuos en regresión lineal
Una forma de estimar los coeficientes de regresión es minimizando la suma de los cuadrados de los residuos:
\[ {a; b}: \min \sum\limits_{i=1}^n \varepsilon_i^2 =\min \sum\limits_{i=1}^n(y_i-(a+bx_i))^2. \]
Derivando e igualando a cero tenemos los siguientes valores que minimizan la función:
\[ b = \frac{s_{xy}}{s_x^2}, \]
\[ a = \bar y - b \bar x. \]
Es inmediato demostrar que la pendiente de la recta también la podemos calcular como:
\[ b = \frac{s_y}{s_x}r_{xy}. \]
3.5.2 Interpretación de los coeficientes
La recta de regresión nos sirve para dos cometidos: explicar la relación entre las variables, y hacer predicciones. En cuanto a la interpretación, el coeficiente \(a\) es el valor medio esperado de \(Y\) cuando \(X=0\). No siempre tiene interpretación ya que el 0 puede estar fuera del dominio de \(X\). El coeficiente \(b\) significa “cuántas unidades aumenta \(Y\) por cada unidad que aumenta \(X\) (si \(b<0\), cuánto disminuye).
En cuanto a la predicción, podemos predecir cuánto valdrá, en promedio, la variable \(Y\) para un determinado valor de \(X, x_{n+1}\). Para hacer la predicción, sustuimos \(x\) por el nuevo valor en la ecuación de la recta:
\[ \hat{y}_{n+1} = a + bx_{n+1}. \]
Hay que tener en cuenta que esta predicción solo es válida para el rango de \(X\) utilizado para obtener los coeficientes.
3.5.3 Error y bondad de ajuste
Pare resumir el error cometido, podríamos buscar una medida resumen de los residuos. Por las propiedades del método de mínimos cuadrados, la media de los residuos es cero:
\[ \bar \varepsilon = \frac{1}{n}\sum\limits_{i=1}^n \varepsilon_i = 0. \]
Entonces, para cuantificar el error, calculamos la media de los residuos al cuadrado, a la que llamamos “varianza residual”:
\[ s_\varepsilon^2= \frac{1}{n}\sum\limits_{i=1}^n \varepsilon_i^2. \]
Si desarrollamos los términos de la varianza residual:
\[ s_\varepsilon^2= \frac{1}{n}\sum\limits_{i=1}^n (y_i - (a + b x_i))^2, \]
llegamos a la siguiente expresión:
\[ \frac{s_\varepsilon^2}{s_y^2}=(1-r_{xy}^2), \]
y de ahí:
\[ r^2_{xy} = 1- \frac{s_\varepsilon^2}{s_y^2} \equiv R^2, \]
que definimos como coeficiente de determinación, y su interpretación es como sigue. La varianza residual \(s_\varepsilon^2\) es la variabilidad no explicada por la recta. Cuanto más se acerquen los puntos a la recta, mejor explicado está el modelo, y más pequeña es esta varianza. La varianza de \(Y\), \(s_y^2\), es la variabilidad Total. Por tanto, \(\frac{s_\varepsilon^2}{s_y^2}\) es la proporción de variabilidad no explicada por la recta de regresión. Y entonces \(R^2\) es la proporción de variabilidad explicada por la regresión.
La expresión general \(R^2 = 1- \frac{s_\varepsilon^2}{s_y^2}\) es válida para cualquier modelo de regresión en el que podamos calcular los residuos y su varianza. Pero la equivalencia \(R^2=r^2\) solo es válida en el caso de la regresión lineal simple.
En el ejemplo de la fábrica de quesos, tomemos \(X\) la variable “materia grasa” e \(Y\) el extracto seco total. Para simplificar el ejemplo, tomamos solo las 15 primeras observaciones, que se muestran en la tabla 3.9. La figura 3.10 muestra la nube de puntos y la recta de regresión estimada por mínimos cuadrados. La recta de regresión estimada es:
\[ \operatorname{\widehat{est}} = 9.509 + 1.696(\operatorname{mg}) \]
El coeficiente \(a\) no tiene interpretación, ya que el cero no es un valor
posible en la variable materia grasa, al menos en esta muestra. La interpretación del coeficiente \(b\) es la siguiente: por cada unidad que aumente mg, porcentaje de materia grasa, aumenta 1.696 unidades est (extracto seco total).
La varianza residual es 0.329, y el coeficiente de determinación:
\[ R^2 = 0,685. \]
Por tanto, la regresión explica el 68,48% de la variabilidad de los datos.
| mg | 14.0 | 13.00 | 13.00 | 13 | 13.50 | 12.50 | 13.0 | 12.50 | 12.5 | 12.50 | 12.50 | 13.00 | 13.50 | 13.50 | 13.50 |
| est | 33.5 | 31.05 | 31.42 | 31 | 31.54 | 30.51 | 32.3 | 31.27 | 31.1 | 30.76 | 30.33 | 31.46 | 31.71 | 33.35 | 32.96 |
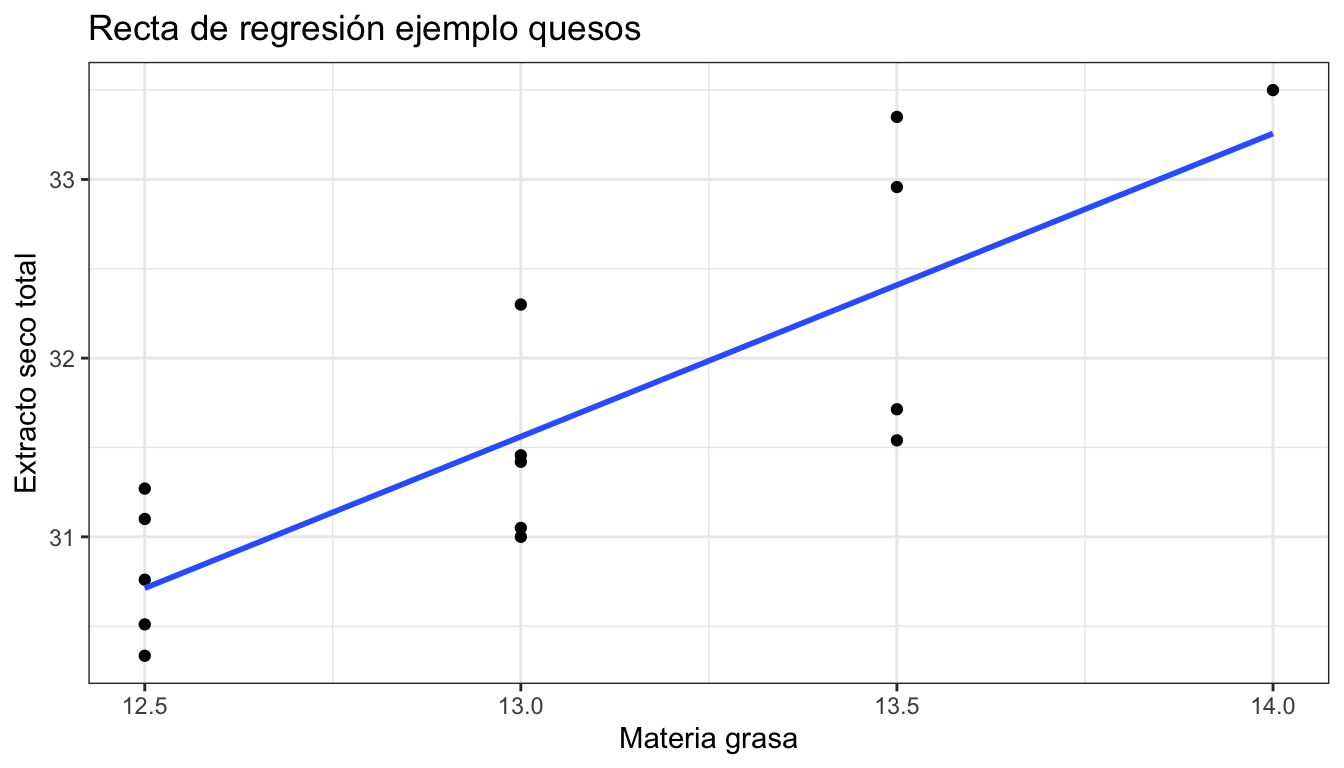
Figura 3.10: Recta de regresión del extracto seco frente a la materia grasa
3.5.4 Extensiones del modelo lineal
El modelo lineal explicado aquí se puede extender fácilmente para recoger algunas relaciones no lineales. Una manera sencilla es aplicar logaritmos a la variable explicativa, a la respuesta o a ambas, y estimar los coeficientes con las variables transformadas. Del mismo modo, se pueden transformar usando potencias o exponenciales, y ajustar polinomios añadiendo términos cuadráticos, cúbicos, etc.
Otra extensión es la regresión multivariante, generalizando a \(p\) variables independientes, que incluso pueden ser cualitativas. Por último, los modelos lineales generalizados pueden estimar modelos con respuestas no continuas, por ejemplo binarias (regresión logística) o de recuentos (regresión de Poisson).
¡Correlación no implica causalidad!
El hecho de que exista relación entre las variables, no significa que esta relación sea de causa-efecto. Para demostrar este tipo de relaciones, sería necesario confirmar con diseño de experimentos.
Visita este enlace para ver algunas correlaciones espúreas (¡y curiosas!).