Capítulo 4 Introducción a la Probabilidad

4.1 Introducción

En los capítulos anteriores, hemos visto cómo mediante la Estadística Descriptiva estudiamos variables estadísticas describiéndolas y representándolas. Mediante la Estadística Inferencial lo que tratamos es de inferir (estimar, predecir) las propiedades de una población basándonos en una muestra de datos. La Teoría de Probabilidades y el Cálculo de Probabilidades son las bases en las que se sustentan estos métodos, partiendo de la estimación del modelo de datos, es decir, la distribución de probabilidad de una determinada característica en la población. En este capítulo estudiaremos los conceptos fundamentales del Cálculo de Probabilidades.

Estándares de aplicación

En este capítulo se han aplicado los siguientes estándares:

• UNE-ISO 3534-1: Estadística. Vocabulario y símbolos. Parte 1, Términos estadísticos generales y términos empleados en el cálculo de probabilidades

Estadística y Cálculo de Probabilidades

La figura 4.1 representa la esencia de la Estadística, esto es, su relación con la probabilidad y la inferencia, a través de la población y la muestra.

Figura 4.1: Relación entre la Estadística Descriptiva, el Cálculo de Probabilidades y la Estadística Inferencial

Es decir, partiendo de los datos de la muestra, estimaremos el modelo de distribución de probabilidad que sigue la variable en estudio en toda la población. A partir de ahí, podremos estimar sus parámetros, calcular probabilidades y realizar contrastes de hipótesis usando técnicas de inferencia estadística. La Estadística Descriptiva sobre los datos de la muestra es una tarea permanente. Necesitamos en primer lugar una definición de la Probabilidad y sus propiedades.

4.2 Sucesos aleatorios

Definamos un experimento como cualquier actividad que deriva en un resultado observable e identificable, al que llamaremos suceso. Estos resultados pueden ser deterministas o aleatorios. Sucesos deterministas son los resultados de aquellos experimentos que, bajo las mismas condiciones, producen el mismo resultado. Por ejemplo, si observamos el número de eclipses de sol que se producen en los próximos 12 meses, el resultado es determinista. Por contra, Sucesos aleatorios son aquellos que están sujetos a incertidumbre. La mayoría de los experimentos no son deterministas sino aleatorios. Por ejemplo, el resultado al lanzar un dado, observar si un cliente compra o no al entrar a una tienda, etc.

Llamamos sucesos elementales a cada uno de los resultados posibles de un experimento. Al ser aleatorios, no conocemos cuál de ellos va a ser el resultado final del experimento, pero sí podemos conocer la probabilidad de que se produzca cada uno de los resultados⁴². Por ejemplo: en una clase de 50 alumnos, si observamos el número de alumnos que obtiene sobresaliente en un curso, no sabemos cuántos van a ser. Pero sí podemos saber cuál es la probabilidad de cada uno de los resultados posibles, en este caso entre 0 (ninguno) y 50 (todos) en base a lo que ha sucedido en años anteriores.

Así, la Probabilidad es una medida del grado de incertidumbre sobre el resultado de un experimento aleatorio. Los posibles resultados de un experimento aleatorio forman un conjunto, y la teoría de probabilidades se sustenta en la teoría de conjuntos. A continuación vamos a definir formalmente los sucesos en términos de conjuntos.

Espacio muestral, \(\Omega\)

Conjunto de todos los resultados posibles

— ISO 3534-1 2.1

\(\Omega\) estará formado por los posibles resultados del experimento o sucesos elementales \(\omega_i\).

Suceso, \(A\)

Subconjunto del espacio muestral

— ISO 3534-1 2.2

Suceso complementario, \(A^c\)

Espacio muestral excluyendo el suceso dado

— ISO 3534-1 2.3

Así, un suceso cualquiera estará formado por uno o varios sucesos elementales \(\omega_i\) del espacio muestral. Un suceso \(A\) ocurre si ocurre alguno de los sucesos elementales que lo componen.

4.2.1 Sucesos notables

Los siguientes sucesos tienen especial importancia en el cálculo de probabilidades:

• Suceso \(A \subseteq \Omega\).
• Suceso complementario⁴³ \(A^c\).
• Suceso seguro \(\Omega\).
• Suceso imposible \(\emptyset\).

La figura 4.2 representa el espacio muestral, un suceso cualquiera \(A\) y su complementario \(A^c\). El suceso imposible no aparece representado, pero en realidad sería:

\[\emptyset = \Omega^c\]

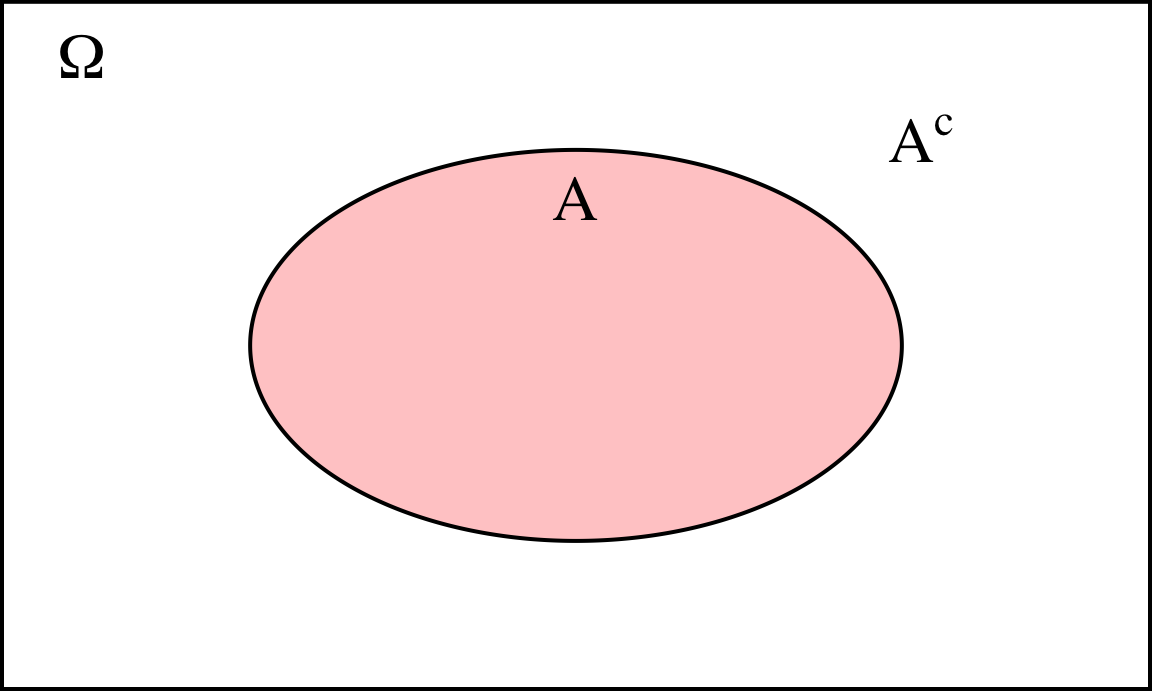
Figura 4.2: Representación del espacio muestral, un suceso cualquiera y su complementario

Habitualmente se utilizan ejemplos de juegos de azar para introducir el cálculo de probabilidades, como lanzamiento de monedas y dados, o combinaciones de cartas en barajas de naipes. Los ejemplos con juegos de azar tienen la ventaja de que son fáciles de comprender.

Lanzamiento de un dado. El experimento consiste en lanzar un dado una vez; Los sucesos elementales son los resultados del 1 al 6; El espacio muestral es el conjunto de todos los sucesos elementales, es decir, \(\Omega = \{1, 2, 3, 4, 5, 6\}\); Si definimos el suceso \(A\) “que salga número par”, entonces \(A = \{2, 4, 6\}\); el suceso \(A\) ocurre si sale un 2, un 4, o un 6.

La aplicación de la probabilidad en casos distintos a los juegos de azar, sigue las mismas leyes, y los ejemplos se pueden asimilar a situaciones reales de la empresa o cualquier otro ámbito. A continuación se describe un ejemplo ilustrativo que, aunque totalmente inventado, se puede encontrar el lector en el futuro con ligeras variaciones según su ámbito de actuación. Utilizaremos en lo posible las cifras usadas en los problemas de azar para ver la utilidad de aquéllos ejemplos en casos más prácticos.

En un estudio se cuenta con un conjunto de 52 sujetos, los cuales están clasificados según alguna característica. Vamos a considerar el experimento de observar un sujeto (por ejemplo cuando entra en la página web del estudio) y clasificarlo según un criterio determinado. Tendremos los siguientes sucesos:

• 52 posibles sujetos en estudio, \((\Omega)\)
• La mitad son mujeres \((M)\)
• 4 investigadores \((I)\) , 12 técnicos \((T)\), resto pacientes \((P)\)
• 13 jóvenes \((J)\), 26 adultos \((A)\), 13 mayores \((R)\); 5, 18 y 3 mujeres en cada grupo respectivamente
• 1 de cada seis hombres \((H)\) responderá al tratamiento \((S)\), el doble si es mujer

¿Con qué juegos de azar relacionarías cada uno de los sucesos anteriores? Piensa algunos ejemplos de sucesos en tu dominio de aplicación con datos similares. El siguiente puede ser un ejemplo más real.

Estudiamos una serie de proyectos de inversión y para ello queremos seleccionar dos de un total de cinco proyectos. El espacio muestral, si asumimos que no nos importa el orden en el que se seleccionan y etiquetamos los proyectos con los números del 1 al 5, es \(\Omega=\{\) (1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5) \(\}\). Es decir, el espacio muestral tiene 10 elementos. El mero recuento se puede realizar mediante técnicas de combinatoria, véase al apéndice D.2. En este caso, \(C_{5, 2} = \binom{5}{2} = 10\).

CALCULADORA

5 \(\boxed{\mathsf{nCr}}\) 2 \(\rightarrow\) 10

HOJA DE CÁLCULO

=COMBIN(5;2) \(\boxed{\mathsf{10}}\)
[EXCEL] =COMBINAT(5;2) \(\boxed{\mathsf{10}}\)

R

La función choose obtiene el número de combinaciones como se ilustra a continuación.

choose(5, 2)
#> [1] 10

4.2.2 Operaciones con sucesos

Como se ha comentado anteriormente, los sucesos son conjuntos. Y como tales, aplican las operaciones y propiedades de la teoría de conjuntos.

Unión de sucesos. Dados dos sucesos \(A\) y \(B\), definimos \(A \cup B\)⁴⁴ como el suceso que se cumple si:

• Ocurre \(A\), o
• Ocurre \(B\), o
• Ocurren \(A\) y \(B\) a la vez

El suceso unión contiene los sucesos elementales comunes y los no comunes, véase la figura 4.3.

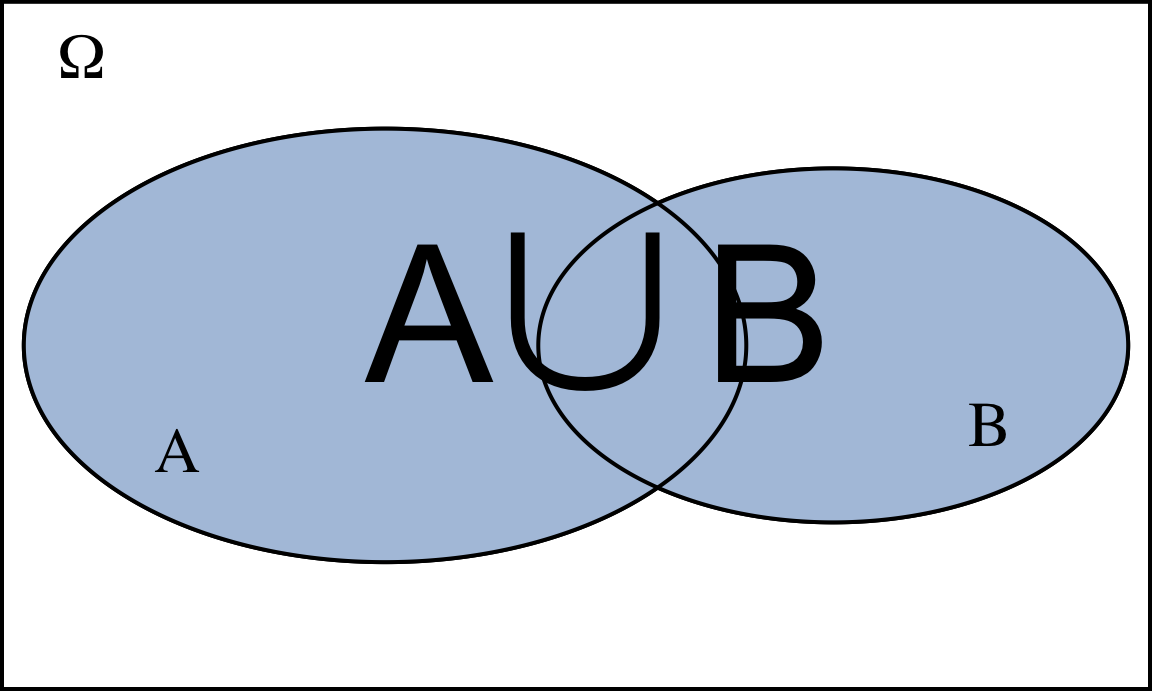
Figura 4.3: Representación de la unión de dos sucesos

El suceso “ser investigador o mujer” en nuestro ejemplo de los sujetos en estudio (\(M \cup I\)) incluirían a lo resultados elementales correspondientes con todas las mujeres (incluidas directivas) y los directivos hombres.

Intersección de sucesos. Dados dos sucesos \(A\) y \(B\), definimos \(A \cap B\)⁴⁵ como el suceso que se cumple si ocurren \(A\) y \(B\) simultáneamente. El suceso intersección contiene únicamente los sucesos elementales comunes a ambos sucesos, véase la figura 4.4.

Las operaciones de unión e intersección entre dos ducesos se extienden inmediatamente a más de dos sucesos.

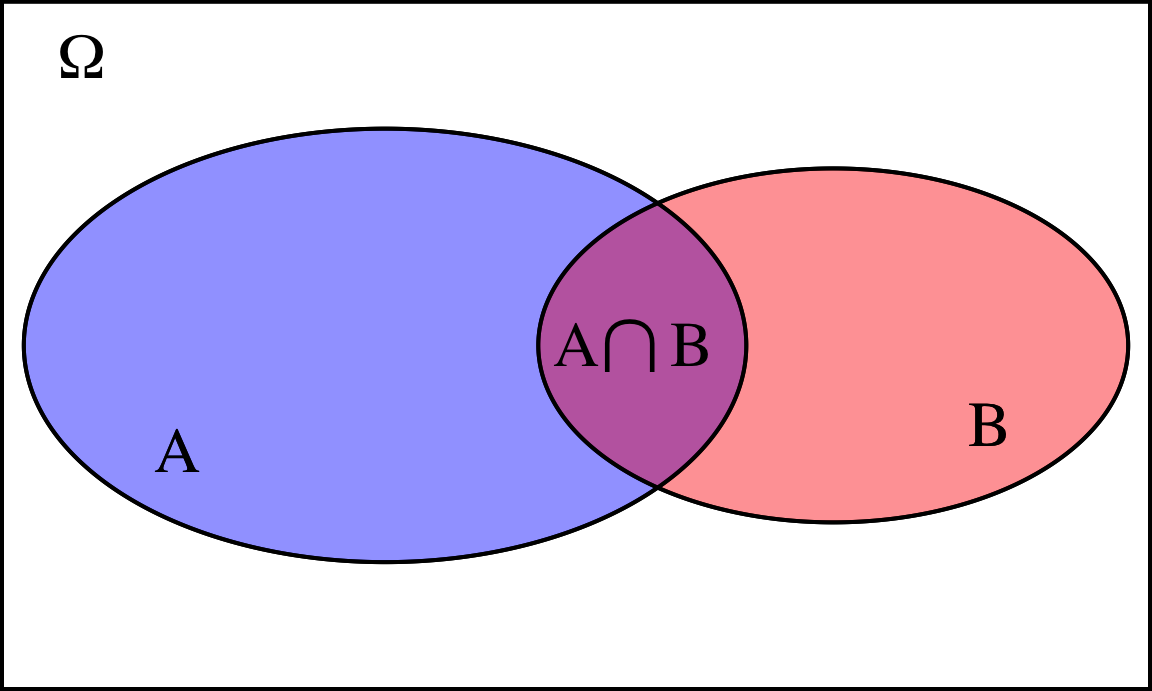
Figura 4.4: Representación de la intersección de dos sucesos

El suceso “ser hombre” y “ser investigador”, se corresponde con la intersección (\(I \cap M^c\)), e incluiría solo a los resultados del experimento en el que los potenciales usuarios hombres son directivos.

Sucesos disjuntos. Dos sucesos \(A\) y \(B\) son disjuntos o mutuamente excluyentes si:

\[A \cap B = \emptyset.\]

Un suceso \(A\) está contenido en otro suceso \(B\), \(A \subset B\) si siempre que se produce \(A\), se produce también \(B\).

Diferencia de sucesos. El suceso diferencia \(A-B\) es el suceso que se produce cuando ocurre \(A\) y no ocurre \(B\). Se verifica:

\[A-B = A\cap B^c.\]

La figura 4.5 muestra una representación de sucesos disjuntos, sucesos incluidos en otros sucesos y diferencia de sucesos.

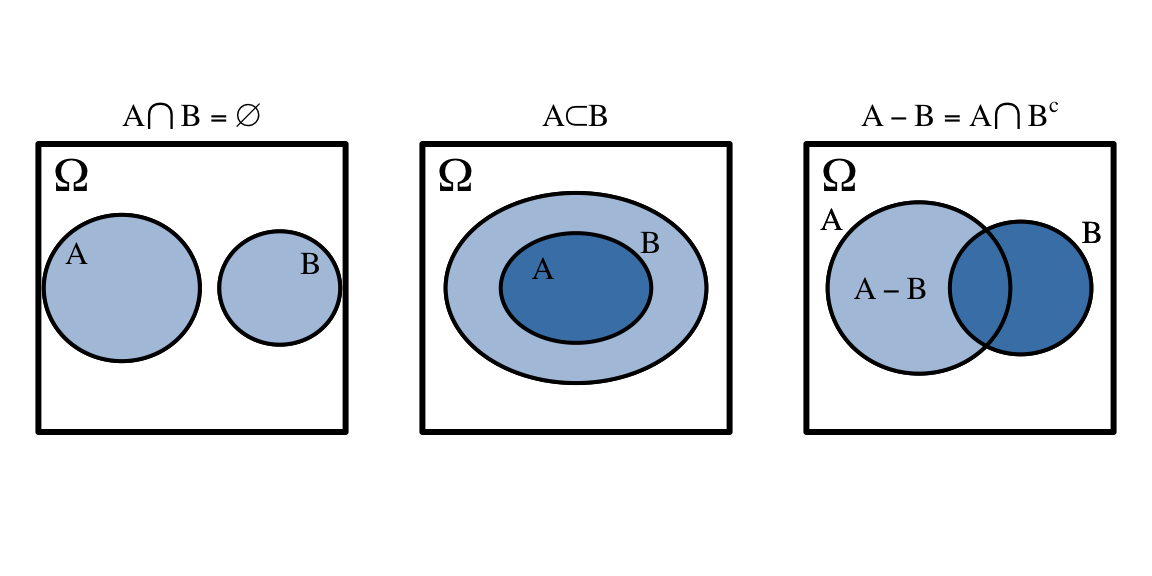
Figura 4.5: Representación de sucesos disjuntos (izquierda), suceso contenido en otro suceso (centro) y diferencia de sucesos (derecha)

El suceso “ser hombre” y el suceso “ser mujer” son sucesos disjuntos (\(H \cap M = \emptyset\)); El suceso “ser mujer joven” está incluido en el suceso “ser mujer”, e incluye a las mujeres jóvenes; El suceso “Ser hombre joven”, se podría representar como \(J-M = J \cap M^c\).

Partición del espacio muestral. Dada una colección de sucesos \(A_1, A_2, \ldots\), decimos que es una partición del espacio muestral \(\Omega\) si:

• \(A_1, A_2, \ldots: \quad A_i \subset \Omega \; \forall i\)
• \(A_i \cap A_j = \emptyset \; \forall i \neq j\),
• \(\displaystyle \underset{i}\bigcup A_i = \Omega\).

La figura 4.6 representa gráficamente una partición del espacio muestral \(\Omega\) en cinco sucesos \(A_1, \ldots, A_5\).

Nótese que los sucesos elementales de un experimento \(\omega_i\) constituyen una partición del espacio muestral.

Figura 4.6: Representación de una partición del espacio muestral

De la teoría de conjuntos se deducen fácilmente las siguientes propiedades de las operaciones con sucesos:

• Conmutativa:
  • \(A\cup B= B\cup A\).
  • \(A\cap B= B\cap A\).
• Asociativa:
  • \(A \cup (B \cup C) = (A \cup B) \cup C\).
  • \(A \cap (B \cap C) = (A \cap B) \cap C\).
• Distributiva:
  • \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\).
  • \(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\).
• Leyes de De Morgan:
  • \((A \cup B)^c = A^c \cap B^c\).
  • \((A \cap B)^c = A^c \cup B^c\).
• \(A \cup A = A \cap A = A \cup \emptyset = A \cap \Omega = A\).
• \(A \cup \Omega = \Omega\).
• \(A \cap \emptyset = \emptyset\).

4.2.3 Clasificación de los espacios muestrales

La primera clasificación que haremos de un espacio muestral es en función de su tamaño:

• Finito: consta de un número finito de sucesos elementales. Por ejemplo el lanzamiento de un dado: \(\Omega = \{1, 2, 3, 4, 5, 6 \}\).

• Infinito numerable: el resultado del experimento tiene (al menos teóricamente) infinitos posibles resultados, pero se pueden numerar. Por ejemplo el número de piezas correctas hasta que se produce un fallo: \(\Omega = \{ 0, 1, 2, 3, \ldots \}\).

• Infinito no numerable: el resultado del experimento tiene infinitos posibles resultados, que no se pueden numerar. Por ejemplo el tiempo hasta el fallo en el ejemplo anterior⁴⁶: \(\Omega = [0, \infty)\).

Otro ejemplo de espacio muestral infinito no numerable consistiría en el resultado de un experimento consistente en realizar una medición de una magnitud continua que pueda tomar cualquier valor entre, por ejemplo, 10 y 20: \(\Omega = x \in \mathbb{R}, 10 \leq x \leq 20\). Una partición de este espacio muestral sería \(A_1 = [10, 15]\), \(A_2 = (15, 20]\).) Nótese que los números (reales, naturales, etc.) son también conjuntos, y por tanto las operaciones relacionadas con sucesos se extienden fácilmente a estos conjuntos.

Definimos una sigma álgebra de sucesos \(\sigma\)-álgebra o \(\aleph\) (aleph) como un conjunto de sucesos que verifican las siguientes propiedades:

• Pertenecen a \(\aleph\),
• Si un suceso pertenece a \(\aleph\), entonces su suceso complementario también pertenece a \(\aleph\),
• Si \(\{A_i\}\) es un conjunto de sucesos en \(\aleph\), entonces la unión \(\displaystyle \underset{i}\bigcup A_i\) y la intersección \(\displaystyle \underset{i}\bigcap A_i\) pertenecen a \(\aleph\).

Nótese la diferencia entre \(\Omega\) y \(\aleph\). Mientras el espacio muestral \(\Omega\) es el conjunto de todos los sucesos elementales del experimento, la \(\sigma\)-álgebra de sucesos \(\aleph\) es el conjunto de todos los sucesos que podemos crear a partir del espacio muestral \(\Omega\) y las operaciones de unión, intersección y complementariedad con esos sucesos. El par \((\Omega, \aleph)\) se dice que es un espacio probabilizable.

Observamos al azar el tipo de participante en el estudio de uno tomado al azar. Entonces los posibles resultados del experimento o sucesos elementales es:

\[\Omega = \{I, T, P\}\]

Haciendo todas las operaciones posibles de unión, intersección y complementariedad, podemos llegar fácilmente a la siguiente \(\sigma\)-álgebra de sucesos:

\[\aleph = \{I, T, P, (I \cup T),(I \cup P), (T \cup P), \emptyset, \Omega \}\]

4.3 Definiciones de probabilidad y sus propiedades

Ya hemos dicho anteriormente que la probabilidad es una medida del grado de incertidumbre sobre el resultado de un experimento. Ahora necesitamos formalizar la definición de probabilidad con el fin de trabajar matemáticamente con ella.

4.3.1 Definición clásica o de Laplace

La definición clásica de la probabilidad, también conocida como definición de Laplace⁴⁷, requiere disponer de un espacio muestral finito referido a un experimento en el que todos los resultados posibles son igualmente probables. Bajo estas condiciones, la probabilidad de un suceso cualquiera \(A\) se obtiene como el cociente entre el número de casos favorables al suceso, dividido por el número total de casos posibles del experimento. Así:

\[P(A) = \frac{\text{casos favorables a } A}{\text{casos posibles}}.\]

Utilizaremos la definición de Laplace para asignar probabilidades a sucesos cuando tengamos una enumeración completa del espacio muestral como en los ejemplos anteriores.

En el lanzamiento de un dado equilibrado de seis caras, la probabilidad de sacar un seis es igual al cociente entre los casos favorables a sacar un 6 (1) y los casos posibles del experimento (6):

\[A:\text{ Sacar un 6 en el lanzamiento de un dado}\]

\[P(A) = \frac{\text{casos favorables a } A}{\text{casos posibles}}= \frac{1}{6} \simeq 0.1667.\]

En el ejemplo de los sujetos en estudio, la probabilidad de que un sujeto al azar sea investigador es el cociente entre los casos favorables a ser investigador (4) y los casos posibles (52):

\[P(I) = \frac{4}{52} = 0.0769\]

Casi dos siglos antes de que Laplace publicara su Teoría Analítica de las probabilidades, Pascal y Fermat intercambiaron correspondencia para intentar resolver los problemas que el Caballero de Méré le planteó al primero. Este personaje era un jugador profesional de la época que planteaba estos problemas en términos de si tenía ventaja al apostar a unos u otros resultados en el lanzamiento de dos dados. Este fue para muchos el origen de la teoría de la probabilidad. Una historia más detallada puede encontrarse en Fernando Corbalán and Gerardo Sanz⁴⁸.

4.3.2 Definición frecuentista o empírica

La definición clásica de probabilidad se encuentra con dificultades para asignar probabilidades a medida que los experimentos alcanzan cierta complejidad. Por una parte, no siempre tenemos una descripción completa del espacio muestral, o, simplemente, es infinito, con lo cual no podemos aplicar la fórmula de Laplace. otras veces no tenemos la información disponible necesaria. Pensemos en la situación habitual descrita en la figura 1.1 al principio de este capítulo. Queremos asignar una probabilidad a un suceso referido a nuestra población objeto de estudio. Sin embargo, no tenemos información de los casos posibles y favorables a la ocurrencia del suceso. A lo sumo, tenemos acceso a una muestra de datos de la población, a la que podemos aplicar el experimento y obtener las frecuencias de ocurrencia de los sucesos en cuestión. Pues bien, la definición frecuentista nos dice que si observamos la frecuencia de ocurrencia del suceso \(A\), llamémosle \(n(A)\), en un número grande de experimentos \(n\), la frecuencia relativa de ocurrencia del suceso \(A\) tiende a la probabilidad del suceso \(A\). Matemáticamente:

\[P(A) = \lim\limits_{n \to \infty} \frac{n(A)}{n}.\]

En experimentos fáciles de realizar, se puede comprobar empíricamente. Por ejemplo, podemos lanzar una moneda e ir anotando la frecuencia de caras con cada repetición. Este tipo de experimentos son también fáciles de realizar mediante simulación. En la siguiente aplicación se puede simular la elección de elementos de un conjunto⁴⁹.

En la práctica, utilizaremos esta definición para asignar probabilidades a sucesos en base a datos históricos, experiencia previa, etc. En muchas ocasiones, estos datos están disponibles en forma de porcentajes, y bastará con dividir por 100 para transformarlos en una frecuencia relativa, que se tomará como probabilidad.

En nuestro ejemplo de los sujetos en estudio, podemos disponer de datos históricos que nos digan que 17 de 100 sujetos varones respondieron al tratamiento en un estudio similar. De ahí podemos asignar al suceso \(A=\) “el sujeto masculino responde al tratamiento” una probabilidad \(P(A)=\frac{17}{100} \approx \frac{1}{6}\), equivalente a “uno de cada 6” que se decía en la descripción del ejemplo.

Históricamente, el 1% de las piezas producidas en una fábrica tienen algún tipo de defecto. Entonces, la probabilidad de que una pieza tomada al azar tenga defecto (\(D\)) es \(P(D) = \frac{1}{100} = 0.01\).

4.3.3 Definición subjetivista

En las dos definiciones anteriores de probabilidad, hemos asignado probabilidades a sucesos en base a unos determinados datos, bien de recuento de posibilidades, bien de frecuencias relativas. En ocasiones, no se dispone de absolutamente ningún dato de este tipo. Entonces las probabilidades se han de asignar de forma subjetiva, fijadas por un individuo en particular como su grado de creencia acerca de la ocurrencia de un suceso. El individuo fija un valor entre cero y uno en base a la evidencia de que dispone, que puede incluir juicios personales, y también interpretaciones a priori sobre las dos concepciones anteriores de la probabilidad, clásica y frecuentista. Por ejemplo, puede considerar la frecuencia relativa de fenómenos similares, y combinar esta información con sus conocimientos y percepciones sobre la materia de estudio.

El enfoque subjetivista tiene especial interés en fenómenos que no se prestan a repetición, así como en métodos de estadística Bayesiana, donde se fija una probabilidad a priori de los parámetros de la población⁵⁰. Existen métodos específicos para asignar probabilidades subjetivas de forma racional, que quedan fuera de los objetivos de este libro, véase, por ejemplo, Bruno de Finetti⁵¹.

¿Cuál es la probabilidad de que me contraten en mi primera entrevista de trabajo? ¿Cuál es la probabilidad de que un proyecto de inversión determinado sea rentable? Podemos asignar probabilidades, pero no tenemos información previa acerca de las frecuencias relativas o casos favorables/posibles.

4.3.4 Definición en ISO 3534-1

La definición estandarizada que proporciona la norma UNE-ISO 3534-1 es la siguiente para la probabilidad de un suceso \(A\):

Probabilidad de un suceso \(A\); \(P(A)\)

Número real del intervalo cerrado \([0, 1]\) asignado a un suceso

— ISO 3534-1 2.5

Nótese que en el estándar no se entra en detalles matemáticos por el bien de la aplicabilidad en los procesos empresariales. No obstante, esta definición es en esencia compatible y congruente con el resto de definiciones de probabilidad.

4.3.5 Definición axiomática

Si bien todas las definiciones anteriores son válidas y útiles en determinados contextos, todas presentaban problemas para desarrollar una teoría de probabilidades que se pudiera aplicar a cualquier espacio probabilizable. La siguiente definición axiomática⁵² resolvió estos problemas.

Una probabilidad \(\wp\) es una función:

\[ \begin{split} \wp: & \; \aleph \longrightarrow [0, 1]\\ & A \longrightarrow P(A) \end{split} \]

que cumple:

1. Primer axioma: \(\forall A \in \aleph \; \exists \; P(A) \geq 0\).

2. Segundo axioma: \(P(\Omega) = 1\).

3. Tercer axioma: Dada la sucesión \(A_1, \ldots, A_i, \ldots: A_i \in \aleph \; \forall\, i, A_i \cap A_j = \emptyset \; \forall i \neq j\), se cumple:

\[P \left (\bigcup\limits_{i=1}^{\infty} A_i \right ) = \sum\limits_{i=1}^{\infty} P(A_i).\]

En lenguaje natural, el primer axioma indica que a cada suceso le podemos asignar un número no negativo llamado “probabilidad del suceso \(A\)”; el segundo axioma asigna al suceso seguro una probabilidad igual a 1; el tercer axioma establece la forma de calcular probabilidades a la unión de sucesos disjuntos o mutuamente excluyentes, mediante la suma de sus respectivas probabilidades. Nótese que la formulación del axioma es válida para espacios muestrales infinitos (numerables y no numerables).

A partir de estos tres axiomas, se deducen los siguientes teoremas:

1. Dados \(n\) sucesos disjuntos dos a dos \(A_1, \ldots, A_n: A_i \cap A_j = \emptyset \; \forall i \neq j\):

\[P \left (\bigcup\limits_{i=1}^{n} A_i \right ) = \sum\limits_{i=1}^{n} P(A_i).\]

2. \(P(A^c)=1-P(A)\).

3. \(P(\emptyset) = 0\).

4. Dados \(A_1, A_2: A_1 \subset A_2 \implies P(A_1) \leq P(A_2)\).

5. \(P(A \cup B) = P(A) + P(B) - P(A \cap B)\).

6. \(P(\bigcup\limits_{i=1}^n A_i) = \sum\limits_{i=1}^n P(A_i) - \sum\limits_{i<j} P(A_i \cap A_j) + \sum\limits_{i<j<k} P(A_i \cap A_j \cap A_k) -\)
   \(- \ldots + (-1)^{n-1} P \left(\bigcap\limits_{i=1}^n A_i\right ).\)

El primer teorema particulariza el tercer axioma a un conjunto finito de sucesos disjuntos del espacio muestral. El segundo teorema es una de las propiedades que más aplicaremos en cálculo de probabilidades, y nos indica cómo calcular la probabilidad de un suceso restándole a 1 la probabilidad de su complementario. El tercer teorema es una consecuencia del anterior y del primer axioma, por los cuales la probabilidad del suceso imposible es cero. El cuarto teorema es de vital importancia cuando trabajemos con variables aleatorias y nos viene a decir que si un suceso está contenido en otro, la probabilidad del primero no puede ser mayor que la del segundo. Los teoremas quinto y sexto nos permiten calcular probabilidades de la unión de cualesquiera conjuntos, sean o no disjuntos. Una consecuencia fundamental de las propiedades de la probabilidad es:

\[ \boxed{0 \leq P(A) \leq 1}.\]

La demostración de estos teoremas se puede encontrar, entre otros, en M. D. Ugarte, A. F. Militino, and A. T. Arnholt⁵³. Asímismo, se puede comprobar fácilmente cómo las definiciones clásicas y frecuentistas cumplen todas estas propiedades y por lo tanto son coherentes con la definición axiomática de la probabilidad.

Lanzamiento de un dado de seis caras. Sean los siguientes sucesos:

• \(A_1:\) “número impar”; \(A_1 = \{1, 3, 5\}\).
• \(A_2:\) “número par”; \(A_2 = \{2, 4, 6\}\).
• \(A_3:\) “número mayor que 4”; \(A_3 = \{5, 6\}\).
• \(A_4:\) “número menor o igual que 4”; \(A_4 = \{1, 2, 3, 4\}\).

Podemos calcular cualquiera de estas probabilidades por la definición de Laplace, ya que los resultados elementales del experimento son equiprobables. Así:

\[P(A_1) = \frac{1}{2}=0.5=P(A_2); P(A_3) = \frac{2}{6}\simeq 0.3333; P(A_4)=\frac{4}{6}\simeq 0.6667.\]

Por simple enumeración de los casos posibles podemos calcular las probabilidades de los siguientes sucesos:

• \(A_1 \cup A_3:\) “número impar o mayor que cuatro”; \(A_1 \cup A_3=\{1,3,5,6\}\); \(P(A_1 \cup A_3)=\frac{4}{6} \simeq 0.6667\).

• \(A_1 \cap A_3:\) “número impar y mayor que cuatro”; \(A_1 \cap A_3=\{5\}\); \(P(A_1 \cap A_3)=\frac{1}{6} \simeq 0.1667\).

• Y así sucesivemente para cada posible suceso \(A\) subconjunto del espacio muestral \(\Omega=\{1,2,3,4,5,6\}\).

Ahora bien, también podemos aplicar las propiedades de la probabilidad sin necesidad de enumerar o contar todas las posibilidades. Por ejemplo, conocidos \(P(A_1), P(A_3)\) Y \(P(A_1\cap A_3)\):

• \(P(A_1 \cup A_3)=P(A_1) + P(A_3) - P(A_1 \cap A_3) = 0.5 + 0.3333 - 0.1667 \simeq 0.6667\),

que conduce, obviamente, al mismo resultado. A medida que aumentan la complejidad de los experimentos, con espacios muestrales más grandes, o incluso infinitos, se hace dificultoso o imposible trabajar con enumeraciones, y es donde hay que aplicar la defición axiomática de la probabilidad.

En nuestro ejemplo del estudio, podríamos estar interesados en el suceso “ser mujer o joven”. Este suceso se correspondería con el suceso \(M \cup J\). Para calcular esta probabilidad, tendríamos en cuenta, según los datos del ejemplo, que \(P(M) = \frac{1}{2}=0.5\), \(P(J) = \frac{13}{52}=0.25\), y \(P(M \cap J)=\frac{5}{52}\simeq 0.0962\). Entonces:

\[P(M \cup J)=P(M)+P(J)-P(M\cap J)=0.5+0.25-0.0962 \simeq 0.6538.\]

En los anteriores ejemplos hemos utilizado solamente el teorema referido a la probabilidad de la unión de sucesos. El teorema de la probabilidad del suceso complementario va a ser la propiedad que más utilizaremos en cálculo de probabilidades, dado que, en muchas ocasiones, es más sencillo abordar el problema desde el punto de vista del suceso complementario. Un ejemplo es la paradoja de los cumpleaños.

Si el día de nuestro cumpleaños asistimos a algún evento en el que haya más de 30 personas, es muy probable que nos canten el cumpleaños feliz a más de una persona. Supongamos una clase de 30 alumnos. ¿Cuál es la probabilidad de que al menos dos alumnos cumplan años el mismo, día?. Abordar el problema directamente implicaría gran cantidad de consideraciones y costosos cálculos hasta llegar a la solución, porque habría que considerar todos los casos posibles y después calcular probabilidades de uniones e intersecciones. Sin embargo, se resuelve de forma casi inmediata sin consideramos la probabilidad del suceso complementario. Es decir, si:

\(A:\) Al menos dos personas de un grupo de 30 cumplen años el mismo día,

entonces el suceso complementario es:

\(A^c\): No hay dos personas en un grupo de 30 que cumplen años el mismo día.

Nótese cómo la probababilidad sería igual a 1 si el grupo de personas fuera de 365 personas o más⁵⁴, ya que en ese caso el suceso sería un suceso seguro. En este caso, el espacio muestral estará compuesto por el número de maneras que tendríamos de ordenar 30 fechas de nacimiento dentro de un año (día-mes), para un conjunto total de 365 días diferentes que tiene el año. Obviamente se pueden repetir las fechas, y por tanto el número total de casos posibles se corresponde con las variaciones con repetición de 365 elementos tomados de 30 en 30:

\[\mathit{VR}_{m,n} = m^n = 365^{30} \simeq 7.392\cdot 10^{76}.\]

Para calcular el número de casos favorables a que nadie cumpla años el mismo día, fijamos el cumpleaños de la primera persona. Entonces la siguiente persona pueden cumplir años cualquiera de los 364 días restantes; fijados los dos primeros, la tercera persona puede cumplir años cualquiera de los 363 días restantes, y así sucesivamente. Por tanto, los casos favorables son las variaciones (sin repetición):

\[\mathit{V}_{m,n}=365\times 364 \times \ldots \times (365-30+1) \simeq 2.171\cdot 10^{76}\]

y entonces:

\[P(A) = 1-P(A^c) = 1- \frac{2.171\cdot 10^{76}}{7.392\cdot 10^{76}}\simeq 0.7063.\] Intuitivamente nos parecería una probabilidad demasiado alta para un grupo tan pequeño de personas, por eso nos sorprendemos cuando escuchamos un cumpleaños feliz el día de nuestro cumpleaños en un lugar concurrido y no es para nosotros. Como vemos, no es tan difícil.

Para obtener los casos favorables, si intentamos utilizar la fórmula de las variaciones utilizando los factoriales (ver apéndice D.2), la calculadora y el software pueden devolver un error, por no poder calcular el factorial de 365.

HOJA DE CÁLCULO

Disponemos en el rango A1:A30 los números del 365 (m) al 336 (m - n + 1). Entonces podemos obtener la probabilidad del ejemplo como:

=1-PRODUCTO(A1:A30)/(365^30)

MAXIMA

Maxima sí puede trabajar con números grandes, la siguiente expresión devuelve la probabilidad pedida:

1 - (factorial(365)/factorial(365-30))/365^30;

R

El siguiente código realiza los cálculos paso a paso y devuelve la probabilidad pedida. Cambiando el valor 30 por otro número de personas cualquiera, se puede ver cómo aumenta la probabilidad.

ncumple <- 30
cposibles <- 365^ncumple
cfavorables <- prod(365:(365 - ncumple + 1))
prob_ninguno <- cfavorables/cposibles
prob_alguno <- 1 - cfavorables/cposibles
prob_alguno
#> [1] 0.7063162

Una vez definida la medida de probabilidad \(\wp\) con los axiomas y propiedades anteriores, llamamos espacio de probabilidad a la terna:

\[(\Omega, \aleph, \wp).\]

El estándar UNE-ISO 3534-1 recoge la definición axiomática de la probabilidad de la siguiente forma:

sigma álgebra de sucesos; \(\sigma\)-álgebra; sigma campo; \(\sigma\)-campo; \(\aleph\)

Conjunto de sucesos con las siguientes propiedades:

1. Pertenecen a \(\aleph\);

2. Si un suceso pertenece a \(\aleph\), entonces su suceso complementario también pertenece a \(\aleph\);

3. Si \(\{A_i\}\) es un conjunto de sucesos en \(\aleph\), entonces la unión \(\displaystyle\underset{i}\bigcup A_i\) y la intersección \(\displaystyle \underset{i}\bigcap A_i\) de los sucesos pertenecen a \(\aleph\).

— ISO 3534-1 2.69

Medida de probabilidad \(\wp\)

Función no negativa definida sobre la sigma álgebra de sucesos tal que

1. \(\wp(\Omega) = 1\)

donde \(\Omega\) denota el espacio muestral

2. \(\wp \left (\bigcup\limits_{i=1}^{\infty} A_i \right ) = \sum\limits_{i=1}^{\infty} \wp(A_i)\)

donde \(\{A_i\}\) es una secuencia de pares de sucesos disjuntos

— ISO 3534-1 2.70

Espacio de probabilidad (o espacio probabilístico); \((\Omega, \aleph, \wp)\)

Espacio muestral, una sigma álgebra de sucesos asociada, y una medida de probabilidad.

— ISO 3534-1 2.68

4.4 Probabilidad condicionada y sus consecuencias

4.4.1 Probabilidad condicionada

El concepto de probabilidad condicionada es uno de los más importantes en teoría de la probabilidad. En ocasiones, la ocurrencia o no de ciertos sucesos del espacio muestral puede estar afectada por otros sucesos del espacio muestral. Por ejemplo, desde el punto de vista de la definición de probabilidad de Laplace, en experimentos secuenciales \(A_1, \ldots, A_n\), es posible que los resultados de los sucesivos experimentos influyan en los resultados de los siguientes, y entonces hablaremos, por ejemplo, de la probabilidad del suceso \(A_2\) condicionada a que ha ocurrido el suceso \(A_1\), y la calcularemos enumerando los casos favorables y los casos posibles bajo el supuesto de haber sucedido \(A_1\). Esta situación aparece, por ejemplo, en los problemas de urnas. Desde el punto de vista de la definición frecuentista de la probabilidad, podemos considerar un experimento en el que se observen un suceso \(A\) en distintos grupos o localizaciones, siendo \(B\) el suceso que indica la pertenencia a ese determinado grupo o característica. Se pueden considerar las frecuencias relativas del suceso \(A\) sólo para aquellos experimentos en los que ha sucedido \(B\), y llamar a estas frecuencias⁵⁵ frecuencias de \(A\) condicionadas a \(B\), \(fr_{A|B}\). Estas frecuencias relativas las podemos calcular dividiendo el número de veces que ocurren tanto \(A\) como \(B\) \((n_{AB})\) entre el número total de veces que ocurre \(B\), \((n_{B})\):

\[fr_{A | B}=\frac{n_{AB}}{n_B}.\]

Ahora bien, como \(fr_A= \frac{n_A}{n}\), \(fr_B= \frac{n_B}{n}\) y \(fr_{AB}= \frac{n_{AB}}{n}\), se tiene:

\[fr_{A | B}=\frac{n\cdot fr_{AB}}{n\cdot fr_B}=\frac{fr_{AB}}{fr_B}.\]

Es decir, la frecuencia condicionada es igual a la frecuencia conjunta dividido por la frecuencia marginal del suceso condicionante. Así pues, dado que para un número grande de realizaciones del experimento, las frecuencias relativas equivalen a la probabilidad, y podemos definir la probabilidad del suceso \(A\) condicionada al suceso \(B\) como:

\[\boxed{P(A | B)=\frac{P(A \cap B)}{P(B)}},\]

siempre y cuando \(P(B) > 0\). Se demuestra fácilmente⁵⁶ que esta definición de probabilidad condicionada cumple que dado un suceso \(A \in \aleph\), \((\Omega, \aleph, \wp(\cdot|A)\) es un espacio de probabilidad.

La tabla 4.1 contiene las frecuencias con las que se han observado los sucesos aprobar y suspender dos elementos evaluables de una asignatura: un examen y un trabajo.

Designemos \(AE\) y \(SE\) a los sucesos “aprobar el examen” y “suspender el examen” respectivamente, y \(AT\) y \(ST\) a los sucesos “aprobar el trabajo” y “suspender” el trabajo respectivamente. La probabilidad de aprobar el examen será:

\[P(AE)=\frac{40}{100} = 0.4.\]

Si incluimos más información a modo de condición, podemos calcular por ejemplo la probabilidad de aprobar el examen condicionado a que se ha aprobado el trabajo:

\[P(AE | AT)=\frac{P(AE \cap AT)}{P(AT)}=\frac{30/100}{35/100} \simeq 0.8571 .\]

Tabla 4.1: Datos ejemplo probabilidad condicionada

	Trabajo aprobado	Trabajo suspenso
Examen aprobado	30	10
Examen suspenso	5	55

En nuestro ejemplo de sujetos en estudio aparece la probabilidad condicionada de la siguiente forma. Se dice que uno de cada seis hombres responde al tratamiento. Si definimos \(S\) como el suceso “responder al tratamiento”, entonces \(P(S|H)=\frac{1}{6}\simeq 0.1667\). Por otra parte, si quisiéramos calcular la probabilidad de que un sujeto sea mujer, condicionado a que es joven, entonces \(P(M | J)=\frac{P(M \cap J)}{P(J)} = \frac{5/52}{13/52}\simeq 0.3846\).

4.4.2 Probabilidad de la intersección de sucesos

La definición de probabilidad condicionada a la que hemos llegado, nos permite calcular la probabilidad de la intersección de dos sucesos cualesquiera sin más que despejar de la fórmula. Además, tendremos dos formas de calcularla, según conozcamos \(P(A|B)\) o \(P(B|A)\):

\[\boxed{P(A\cap B)=P(A|B)\cdot P(B)=P(B|A)\cdot P(A)}.\]

Recuerda que \(A \cap B\) significa A y B, mientras que \(A|B\) significa A si ocurre B.

La probabilidad condicionada aparece en los muestreos sin reemplazamiento. Se suele asociar a los problemas de urnas, o también a la extracción de cartas de una baraja. Por ejemplo, podemos calcular la probabilidad de sacar dos figuras seguidas de una baraja de cartas francesa, con 52 cartas en total de las cuales 12 son figuras (J, Q, K de cada uno de los cuatro palos). Entonces, si definimos \(A_1\) como “sacar figura en la primera extracción” y \(A_2\) como “sacar figura en la segunda extracción”, entonces lo que buscamos es la probabilidad de que ocurran los dos sucesos, \(P(A_1 \cap A_2)\):

\[P(A_1 \cap A_2)=P(A_1)\cdot P(A_2 | A_1)=\frac{12}{52}\cdot \frac{11}{51}=\frac{11}{221}\simeq 0.0498.\]

En nuestro ejemplo de los sujetos en estudio, ¿cuál es la probabilidad de que un sujeto al azar sea mujer y además responda al tratamiento?

\[P(M \cap S) = P(S|M)\cdot P(M) = \frac{2}{6}\cdot \frac{1}{2} = \frac{1}{6}\simeq 0.1667.\]

A partir de la probabilidad condicionada se llega a la regla de la cadena para calcular la probabilidad de la intersección de una serie de sucesos. La regla consiste en ir multiplicando cada vez la probabilidad del suceso \(A_i\) condicionada a la intersección de todos los anteriores.

\[P\left( \bigcap\limits_{i=1}^{n} A_i \right) = P(A_1)\cdot P(A_2|A_1)\cdot P(A_3|A_1 \cap A_2)\cdot\ldots\cdot P\left(A_n | \bigcap\limits_{i=1}^{n-1} S_i \right). \]

Por ejemplo, en una urna hay 5 bolas rojas y 3 bolas blancas. Hacemos 3 extracciones. Si en una extracción sale blanca, devolvemos la bola a la urna y metemos 2 bolas blancas adicionales. ¿Qué probabilidad hay de sacar 3 blancas seguidas?

Si definimos los sucesos \(A_1\), \(A_2\) y \(A_3\) como “sacar bola blanca en la primera, segunda y tercera extracción respectivamente”, entonces estamos buscando:

\[P(A_1 \cap A_2 \cap A_3),\] que utilizando la regla de la cadena calcularemos como:

\[P(A_1)\cdot P(A_2|A_1) \cdot P(A_3|A_1 \cap A_2).\]

En la situación inicial hay 3 de ocho bolas blancas. En el segundo experimento, si hemos sacado blanca, la devolvemos y añadimos dos más, es decir tenemos 5 de diez bolas blancas. si la segunda vuelve a ser blanca, entonces en el tercer experimento tenemos 7 de 12 bolas blancas. Por lo tanto:

\[P(A_1 \cap A_2 \cap A_3)= \frac{3}{8}\cdot \frac{5}{10} \cdot \frac{7}{12}=\frac{7}{64}\simeq 0.1094.\]

4.4.3 Independencia de sucesos

Si bien en muchas ocasiones el conocimiento de ciertos eventos afectan a la probabilidad de ocurrencia de otros, esto no siempre tiene por qué ser así. En estos casos, diremos que dos sucesos son independientes si el conocimiento de la ocurrencia de uno de ellos no modifica la probabilidad de aparición del otro. Por tanto, en esos casos:

\[P(A|B) = P(A)\quad \text{y}\quad P(B|A) = P(B).\]

Entonces, por la propia definición de la probabilidad condicionada, se tiene que si dos sucesos son independientes, entonces:

\[\boxed{P(A\cap B)=P(A)\cdot P(B)}.\] Esta fórmula, que es una definición en sí misma de independendencia de sucesos, nos proporciona también un método para comprobar si dos sucesos son independientes o no conocidas las probabilidades de los mismos y la de la intersección⁵⁷.

Para más de dos sucesos, la regla de la cadena explicada más arriba se extiende inmediatamente de forma que la probabilidad de la intersección de \(n\) sucesos independientes es el producto de sus probabilidades:

\[P(A_1\cap \ldots \cap A_n)=P(A_1) \cdot \ldots \cdot P(A_n).\] Y en el caso particular de que los \(n\) sucesos sean equiprobables, tales que \(P(A_i) = p \;\forall i\), entonces:

\[P(A_1\cap \ldots \cap A_n)=p^n.\]

El lanzamiento sucesivo de una moneda o de un dado son claros ejemplos de sucesos independientes.

En el lanzamiento de un dado dos veces seguidas (o lo que es lo mismo, en el lanzamiento de dos dados), el resultado del primero no influye en el segundo. Por tanto, la probabilidad de sacar dos seises en el lanzamiento de dos dados es:

\[P(A_1 \cap A_2)= \frac{1}{6}\cdot \frac{1}{6}=\frac{1}{36}\simeq 0.0278.\] Nótese que podemos llegar fácilmente al mismo resultado enumerando los posibles resultados, pero con más esfuerzo. Además, en espacios muestrales más grandes se complica enormemente la enumeración.

4.4.4 Probabilidad condicionada e independencia en ISO 3534-1

La norma UNE-ISO 3534-1 recoge las definiciones de probabilidad condicionada e independencia de la siguiente forma:

Probabilidad condicionada; \(P(A|B)\)

Probabilidad de la intersección de \(A\) y \(B\) dividida por la probabilidad de \(B\).

— ISO 3534-1 2.6

Sucesos independientes

Par de sucesos tal que la probabilidad de la intersección de los dos sucesos es el producto de las probabilidades individuales.

— ISO 3534-1 2.4

4.4.5 Probabilidad total y fórmula de Bayes

La probabilidad condicionada nos permite calcular probabilidades de sucesos de los que tenemos información parcial, en el sentido de que conocemos su probabilidad condicionada a algún otro suceso del espacio muestral, pero queremos saber la probabilidad total del suceso, independientemente de aquellos sucesos. Las condiciones para que podamos calcular la probabilidad total de este suceso, llamémosle \(B\), son:

• Disponer de una partición de sucesos del espacio muestral \(A_1, A_2, \ldots, A_n\) tales que \(A_i \cap A_j = \emptyset \; \forall i \neq j\) y \(\displaystyle \underset{i=1}{\overset{n}\bigcup A_i} = \Omega\).

• Conocer las probabilidades de cada uno de esos sucesos que forman la partición, \(P(A_i)\).

• Conocer las probabilidades del suceso de interés condicionadas a cada uno de los sucesos que forman la partición del espacio muestral, es decir, \(P(B|A_i)\).

Entonces, según el teorema de la probabilidad total, se verifica que:

\[\boxed{P(B)=\sum\limits_{i=1}^{n} P(B/A_i)\cdot P(A_i)}.\] En efecto, podemos ver gráficamente en la figura 4.7 que cada sumando de la fórmula de la probabilidad total se corresponde con las intersecciones del suceso de interés \(B\) con cada uno de los sucesos de la partición \(A_i\). Como estas intersecciones son sucesos disjuntos, la probabilidad de su unión es la suma de sus probabilidades por las propiedades de la probabilidad.

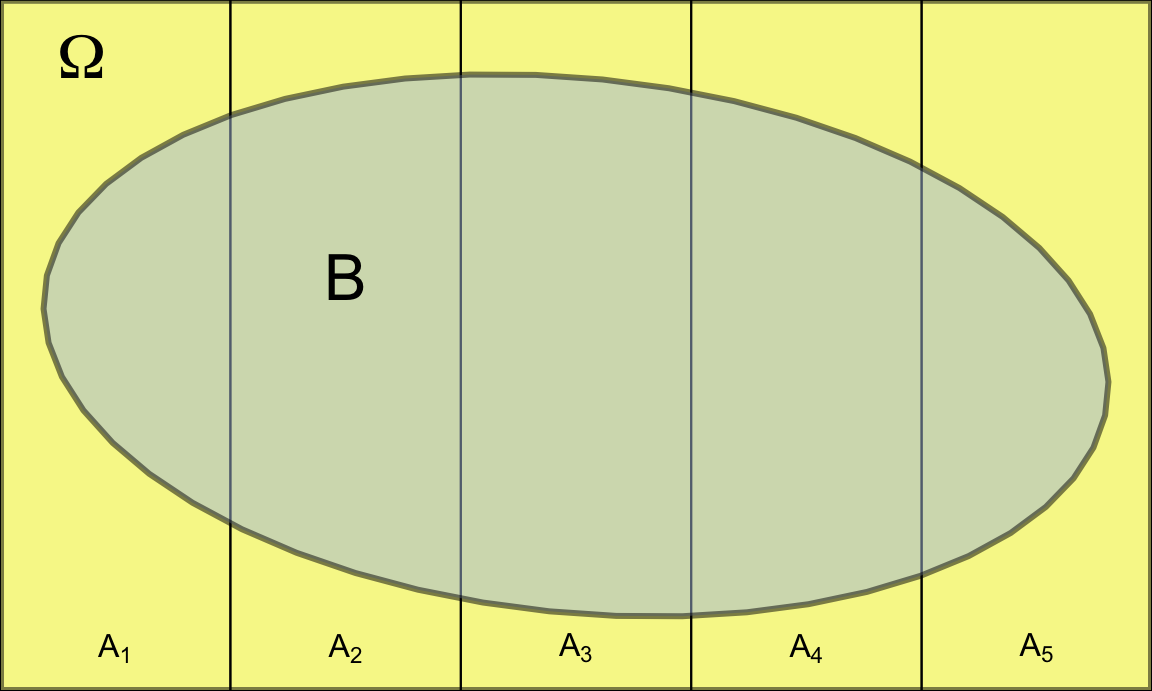
Figura 4.7: Representación del espacio muestral particionado más otro suceso

El desarrollo de la fórmula de la probabilidad condicionada a partir de la situación descrita para calcular la probabilidad total, nos permite darle la vuelta a la condición y encontrar probabilidades de los sucesos de la partición \(A_i\) condicionados a que se haya producido el suceso \(B\). Partimos de la propia definición de \(P(A_i|B)\):

\[P(A_i|B)=\frac{P(A_i\cap B)}{P(B)}.\] Pero a su vez, la probabilidad del numerador la podemos escribir como \(P(A_i \cap B)=P(B|A_i)\cdot P(A_i)\), y la probabilidad del denominador, aplicando la fórmula de la probabilidad total, es \(P(B)=\sum\limits_{i=1}^{n} P(B/A_i)\cdot P(A_i).\) Lo que da lugar a la fórmula de Bayes o Teorema de Bayes:

\[\boxed{P(A_i|B)=\frac{P(B|A_i)\cdot P(A_i)}{\sum\limits_{i=1}^{n} P(B/A_i)\cdot P(A_i)}},\] siempre que \(P(B>0)\), que se puede expresar de forma simplificada como:

\[\boxed{P(A_i|B)=\frac{P(B|A_i)\cdot P(A_i)}{P(B)}}\]

En una empresa que produce componentes electrónicos tomamos 5 lotes de producto, cada uno compuesto de 50 componentes. Hay dos tipos de lotes. Los del tipo 1 (\(A_1\)) tienen 48 componentes correctos y 2 defectuosos. Los del tipo 2 (\(A_2\)) tienen 45 componentes correctos y 5 defectuosos. Tenemos 3 lotes tipo 1 y 2 lotes tipo 2. Si se toma uno de los 5 lotes al azar y se saca de éste una pieza, ¿qué probabilidad hay de que ese componente sea defectuoso?

La figura 4.8 representa la partición del espacio muestral de este ejemplo.

En este ejemplo se dan todos los elementos que habíamos descrito para calcular la probabilidad total del suceso \(B:\) “el componente es defectuosos”. Tenemos información parcial, en el sentido de que conocemos las probabilidades de ser defectuoso para cada uno de los tipos de lote, es decir \(P(B|A_1)=\frac{2}{50}=0.04\) y \(P(B|A_2)=\frac{5}{50}=0.1\). También conocemos las probabilidades de los dos sucesos que constituyen la partición, \(P(A_1) = \frac{3}{5}=0.6\) y \(P(A_2) = \frac{2}{5}=0.4\). Entonces, por el teorema de la probabilidad total:

\[P(B)=P(B|A_1)\cdot P(A_1) + P(B|A_2)\cdot P(A_2)= \\=0.04\cdot 0.6 + 0.1\cdot 0.4=0.064.\]

Supongamos ahora que se extrae del conjunto de todos los lotes un componente al azar, y resulta que es defectuoso. ¿Cuál es la probabilidad de que esa pieza provenga de un lote del tipo 1?

Nótese que ahora lo que buscamos es \(P(A_1|B)\), como conocemos las \(P(B|A_i)\) y \(P(A_i)\), entonces podemos aplicar la fórmula de Bayes. Como ya hemos calculado antes la probabilidad total de \(B\), podemos usar la fórmula abreviada:

\[P(A_1|B)=\frac{P(B|A_1)\cdot P(A_1)}{P(B)}=\frac{0.04\cdot 0.6}{0.064}=0.375.\]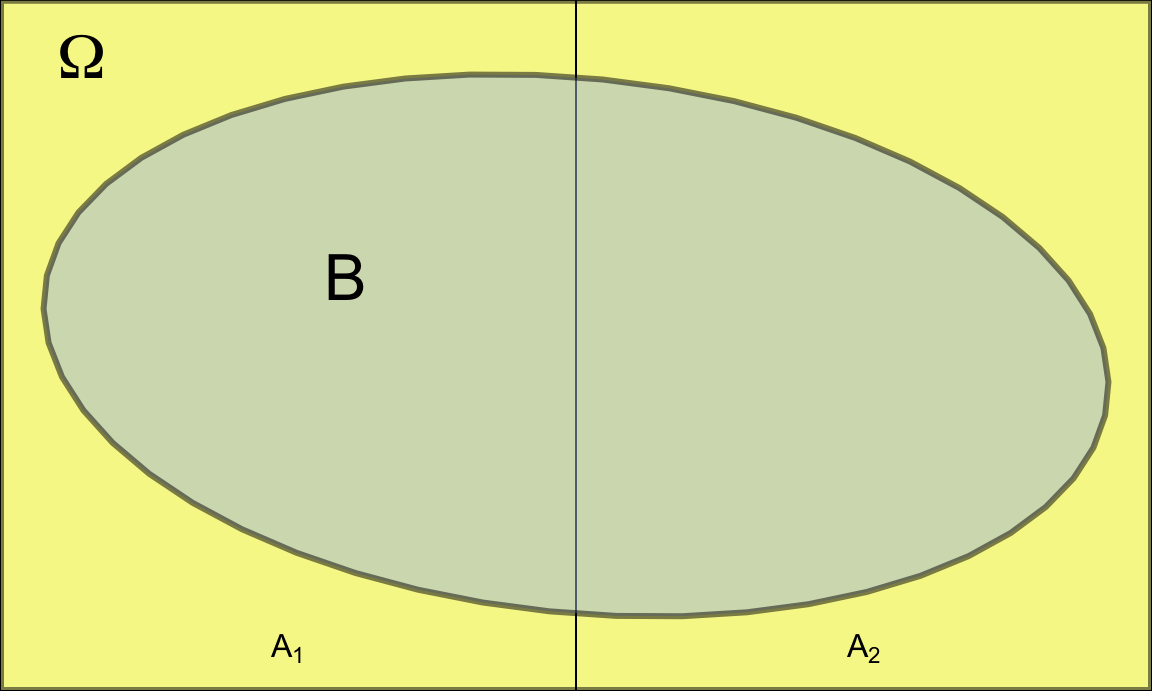

Figura 4.8: Representación del espacio muestral del ejemplo de los componentes electrónicos

En nuestro ejemplo, conocíamos las probabilidades de que un sujeto responda al tratamiento según si es hombre o mujer. También conocemos la probabilidad de que el sujeto sea hombre o mujer. Entonces podemos calcular la probabilidad de que un sujeto (independientemente de si es hombre o mujer) responda al tratamiento como:

\[P(S)=P(S|M)\cdot P(M) + P(S|H)\cdot P(H)= \frac{2}{6}\cdot \frac{1}{2} + \frac{1}{6}\cdot \frac{1}{2} = 0.25.\]

Si un sujeto responde al tratamiento, la probabilidad de que sea mujer es:

\[P(M|S)=\frac{P(S|M)\cdot P(M)}{P(S)}=\frac{\frac{2}{6}\cdot 0.5}{0.25} \simeq 0.6667.\]

El problema de Monty Hall

Monty Hall es el nombre del presentador del concurso televisivo estadounidense Let’s make a deal que se emitió entre 1963 y 1990. En alguna de las fases del programa, el concursante tiene que elegir una entre tres puertas, dos de las cuales tienen detrás una cabra, mientras que la otra tiene un coche. Una vez elegida la puerta, el presentador muestra el contenido de una de las otras dos puertas, que contiene una cabra. Entonces el concursante tiene la opción de cambiar su puerta por la otra que queda cerrada. ¿Es más ventajoso cambiar de puerta o quedarse con la elegida inicialmente? ¿O da lo mismo?

La solución puede parecer contraintuitiva, aunque tanto desde el razonamiento a través de las frecuencias como con un desarrollo matemático se llega a la misma conclusión. Y la clave está en la probabilidad condicionada.

El problema de Monty Hall dio lugar a historias curiosas que se pueden consultar en Corbalán and Sanz⁵⁸. Por ejemplo, el gran matemático Paul Erdös solo aceptó como buena la solución real tras comprobarla en una simulación por ordenador. Invito al lector a que concurse en la aplicación del siguiente enlace⁵⁹ durante un buen número de jugadas y compruebe a través de las frecuencias relativas qué estrategia ofrece mayor probabilidad de ganar el coche.