Capítulo 14 Control Estadístico de Procesos

14.1 Gráficos de control

14.1.1 Introducción

El objetivo de los gráficos de control es identificar cuándo el proceso está fuera de control estadístico. A partir de ahí, los métodos de SPC nos permitirán mejorar el proceso, por medio de la eliminación de las causas asignables de variación.

Assignable causes of variation may be found and eliminated

Walter A. Shewhart

Recordemos de la introducción que los procesos se mueven de forma natural dentro de unos límites de referencia. En los gráficos de control, lo que haremos será tomar muestras de los procesos y medir alguna característica (variable o atributo). Los valores de las muestras los resumiremos con algún estadístico, como la media o la desviación típica. Esta medida resumen la representaremos gráficamente junto con unos límites de control, que abarcan esa franja de variación natural de esa medida resumen. Mientras los valores de la muestra estén dentro de los límites de control, el proceso se puede considerar bajo control estadístico. En los siguientes apartados describiremos con detalle aspectos generales de los gráficos de control, así como gráficos de control específicos.

14.1.1.1 Elementos del gráfico de control

El gráfico de control es un gráfico en dos dimensiones, donde el eje vertical representa una medida resumen de la característica media en las muestras obtenidas del proceso. Dicha medida resumen se refiere a la medición de una característica de interés en los elementos de cada muestra. Sobre ese eje, se representan tres líneas: la línea central (LC, Línea central) y los límites de control superior (LCS) e inferior (LCI)¹⁰⁴. La línea central representa alguna medida de centralización de la medida resumen que se está representado, por ejemplo la media. Los límites de control superior e inferior representan los límites de variación natural de dicha medida resumen, que generalmente se fijan en tres desviaciones típicas¹⁰⁵ a ambos lados del valor central. Estos límites aseguran que, con el proceso bajo control, es muy improbable que un punto se salga de los límites. Por tanto, tendremos mucha seguridad de que el proceso ha dejado de estar bajo control estadśitico. Por ejemplo, para el gráfico de la media, que sigue una distribución normal, la probabilidad de que la media de una muestra se salga de los límites estando el proceso bajo control, es de 0.0027. Es decir, solo el 0.27% de los puntos que se salgan serán una falsa alarma. Una vez representados los límites, situamos los puntos según el valor de la medida resumen de la muestra en el eje vertical, y por orden secuencial según el eje horizontal. Finalmente se unen los puntos con líneas. La figura 14.1 muestra todos los elementos del gráfico de control descritos.

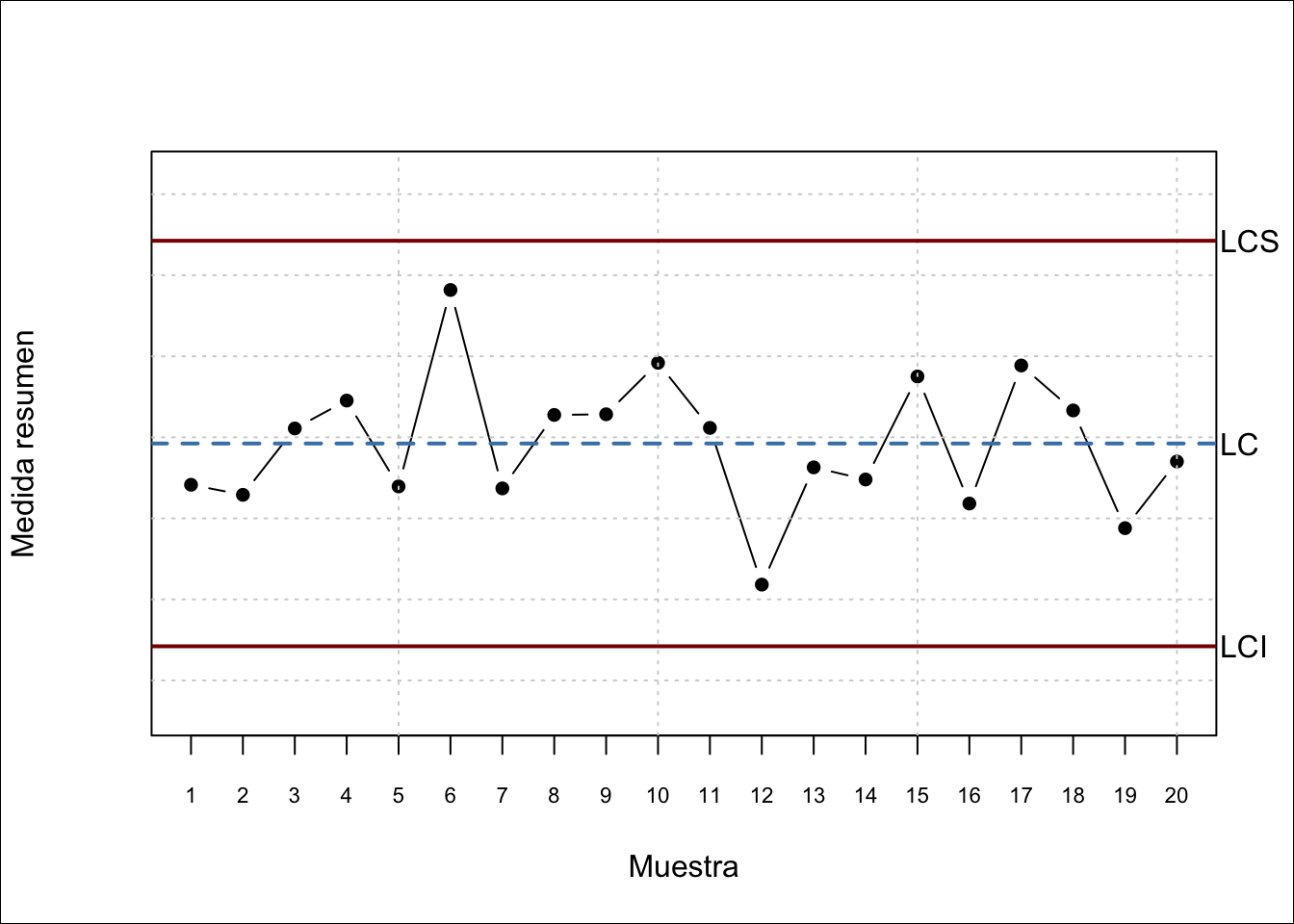
Figura 14.1: Elementos del gráfico de control

14.1.1.2 Diseño del gráfico de control

Una vez determinada la característica de interés, hay dos partes fundamentales del diseño del gráfico de control: la determinación de los límites de control, y la determinación de la estrategia de muestreo. Básicamente, la implementación del gráfico de control se realiza en dos fases:

1. Fase I. Se fijan unos límites de control con el proceso bajo control estadístico.

2. Fase II. Una vez fijados los límites de control, los siguientes valores que produzca el proceso se monitorizan con los límites fijados.

La fase I es la más delicada, y hay varias formas de afrontarla. La más sencilla, es partir de unos valores pre-especificados basados en la media y la desviación típica del proceso. Cuando el proceso es estable, podemos confirmar mediante contrastes de hipótesis que efectivamente esos valores pre-especificados pueden ser los del proceso con una cierta confianza. Cuando no podemos confiar en unos valores pre-especificados, entonces tenemos que estimarlos, fijando así unos límites provisionales utilizando un conjunto de datos preliminar. En general, entre 25 y 30 muestras con entorno a 5 unidadades cada una suele ser suficiente para estimar los límites de control. Si el proceso muestra control estadístico, podemos utilizar esos límites como límites del proceso. Si el proceso no está bajo control estadístico, se eliminan las causas especiales de variación¹⁰⁶ y se vuelven a calcular los límites. Esta operación se repite hasta que el proceso esté bajo control estadístico. Otro aspecto importante de la Fase I es que se debe controlar primero la variabilidad del proceso y, una vez esta variabilidad está bajo control estadístico, comprobar que la media del proceso está también bajo control.

En la Fase II se identifican las causas especiales de variación, que no solo vienen dadas por puntos fuera de los límites, sino también por otros patrones altamente improbables que indiquen que la variación no es debida solamente al azar. Además, en la Fase II se debe vigilar que los límites de control siguen siendo válidos para nuestro proceso, y cuando el proceso cambie, los límites de control se deben revisar y actualizar. De otro modo, el gráfico de control perdería utilidad.

Un error muy común que hay que evitar, es fijar los límites de control con cada nueva muestra de datos. Esto implica que si se producen cambios en el proceso, podemos no detectarlos porque esos datos malos están siendo utilizados para calcular los límites del proceso supuestamente bajo control.

Es importante diferenciar entre control del proceso y especificación del proceso. Es un error muy común no hacerlo, lo que lleva a un uso inadecuado del control estadístico de procesos. El proceso puede no estar controlado pero cumplir las especificaciones, y viceversa. El control estadístico de procesos nos sirve para anticipar futuros problemas que hagan al proceso dejar de cumplir las especificaciones, y poder corregir los problemas antes de que lleguen al producto (y al cliente). Por tanto los límites de control del proceso (fijados por la variación natural del proceso) y los límites de especificación del proceso (fijados por el cliente, ya sea interno o externo), no están relacionados entre sí, son cosas distintas cuya comparación nos permitirá medir la capacidad del proceso, como veremos en el capítulo 14.2.

En cuanto a la estrategia de muestreo, hay varios aspectos básicos que debemos tener en cuenta. El primero, es que la muestra debe ser representativa de la producción. Para ello, se deben realizar muestreos aleatorios. No siempre es posible hacer un muestreo completamente aleatorio, por sorteo, pero sí se deben evitar el tomar muestras que no sean representativas (por ejemplo, tomar siempre las primeras o las últimas del día porque es más cómodo). Por otro lado, se debe realizar una adecuada estratificación. Es decir, debemos tomar las muestras de grupos homogéneos, y no mezclar muestras de partes del proceso diferentes (por ejemplo diferentes máquinas, diferentes turnos, etc.). Por último, hay tres decisiones importantes: cuántas muestras analizar cada vez, de qué tamaño, y cada cuánto tiempo.

Ya hemos dicho que para la determinación de los límites de control se deben utilizar entre 25 y 30 muestras. En general, este es un número adecuado de muestras para representar en cualquier gráfico de control para una fácil lectura e interpretación. No obstante, se puede examinar el gráfico de control con cada nueva observación, junto, por ejemplo, con las 24 anteriores. Las decisiones sobre el tamaño y la frecuencia de la muestra suelen estar muy relacionadas. Para los gráficos que vamos a estudiar en este capítulo, muestras de entre 4 y 8 unidades suelen dar un buen resultado. La frecuencia dependerá de cuánto tiempo estamos dispuestos a esperar hasta detectar un cambio en el proceso. En el apartado 14.1.2 se proporcionan algunas herramientas para determinar el tamaño de la muestra y el error cometido para el gráfico de control de la media, que se puede utilizar para el diseño de un plan de control.

14.1.1.3 Funcionamiento del gráfico de control

Lo que estamos haciendo al controlar los procesos mediante gráficos de control es realmente un contraste continuado de hipótesis para comprobar si el proceso está bajo control. El proceso está bajo control si la variación que se observa no se puede achacar más que al azar. El contraste se aplica a muestras recogidas periódicamente. Si la hipótesis es cierta, la media y la desviación típica de la muestra estarán dentro de sus límites naturales, asumiendo por defecto que estos límites son entre tres desviaciones por encima y por debajo de la media (\(\theta_0 \pm 3\sigma\))¹⁰⁷. Además de los puntos fuera de los límites, hay otras situaciones altamente improbables que también indican que el proceso no está bajo control. Así, los pasos a seguir son los siguientes.

1. Fijar límites con el proceso bajo control
2. Obtener muestras homogéneas (grupos racionales)
3. Calcular medias y desviaciones típicas (o rangos)
4. Representar datos
5. Identificar las situaciones fuera de control
6. Eliminar las causas de variación asignables

Una vez tenemos un adecuado plan de control, debemos fijar los límites del proceso bajo control. A partir de aquí, obtener los gráficos de control con la regularidad establecida en el plan. El plan debe incluir una revisión periódica de los límites de control, y ajustarlos cuando nuestro proceso cambie (en media o en variabilidad). El objetivo de los gráficos de control es detectar causas especiales de variación, y eliminar estas causas. El método descansa en la base de que cualquiera de las situaciones en las que el proceso se clasifica como fuera de control, es tan improbable que suceda, que no podemos aceptar que se deba exclusivamente al azar, es decir, a la variación natural del proceso (causas naturales), y por tanto debe haber otros motivos (causas especiales) que debemos identificar. Por ejemplo, un punto fuera de los límites sólo se producirá de forma natural 27 veces de cada 10.000.

En relación a los efectos producidos por un proceso fuera de control, hay que tener en cuenta que pueden ser diversos. El más intuitivo es que puede provocar una disminución en la capacidad del proceso y por tanto aumentar la proporción de no conformidades a largo plazo. En otros casos puede suceder lo contrario, que se produzca una mejora en el proceso. Si esta mejora no es apreciada por el cliente podemos estar incurriendo en un sobrecoste. Si la mejora es apreciada por el cliente, es una oportunidad para hacer sostenible en el tiempo esa mejora. Por ejemplo, en un proceso donde se mejora la resistencia de un material en un día determinado, si la causa asignable es que se ha añadido más cantidad de la necesaria de un componente determinado, la situación fuera de control supuso un sobrecoste. Si la causa asignable fue un cambio en el procedimiento, se puede implementar el cambio para mejorar el proceso de forma sostenible.

Las siguientes señales nos pueden estar indicando que el proceso deja de estar bajo control. Básicamente, el hecho de que alguno de los siguientes hechos suceda es altamente improbable, por lo que muy posiblemente no se deba al azar, sino a alguna causa especial:

• Puntos fuera de los límites
• Siete puntos seguidos al mismo lado de la línea
• Seis puntos seguidos creciendo o decreciendo
• Catorce puntos seguidos alternando arriba y abajo
• Cualquier otro patrón inusual

Además de estos patrones, se puede mirar dentro de los límites para anticipar posibles problemas. Definimos tres zonas y miramos qué pasa en ellas:

1. Zona C: entre la línea central y una desviación típica
2. Zona B: Entre una y dos desviaciones típicas desde la línea central
3. Zona A: Entre dos y tres desviaciones típicas de la línea central

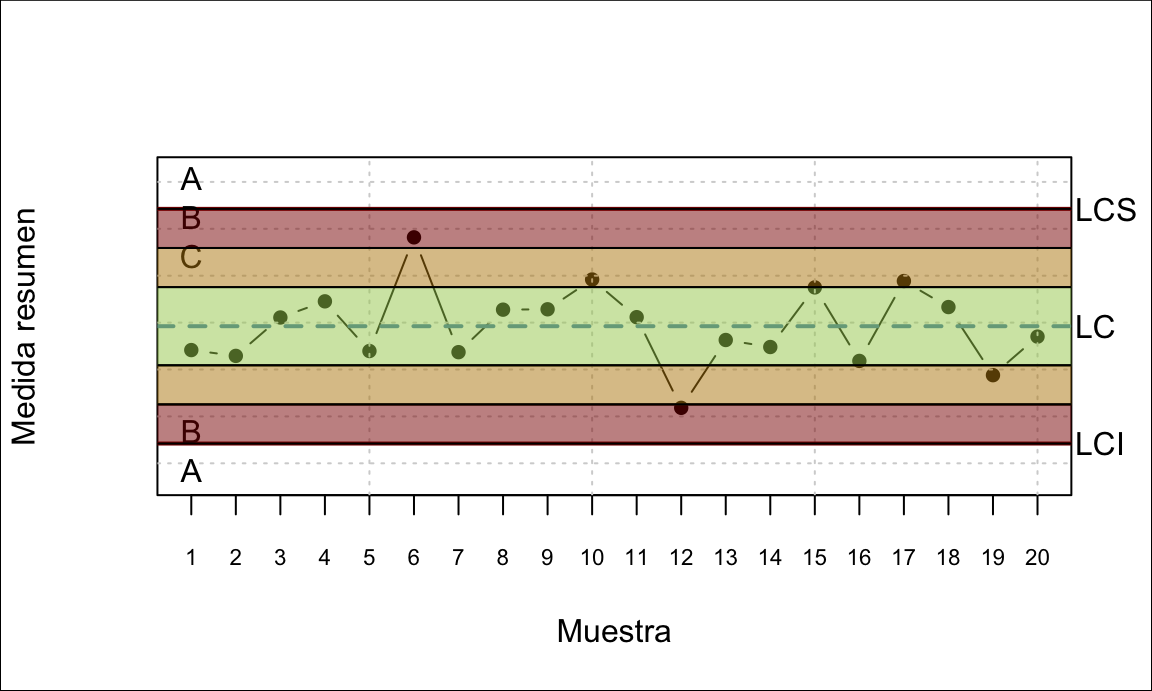
Figura 14.2: Zonas del gráfico de control

Las situaciones que, por ser altamente improbables, se deberían investigar en busca de causas asignables, son las siguientes:

• Dos de tres puntos seguidos en la zona A o más allá
• Cuatro de cinco puntos seguidos en la zona B o más allá
• Quince puntos seguidos en la zona C

El tercer caso es una oportunidad de mejora, ya que se ha conseguido reducir la variabilidad del proceso.

14.1.2 Gráficos de control por variables

Cuando la característica que estamos midiendo es una variable numérica continua, utilizamos gráficos de control por variables. En el control por variables, debemos controlar tanto los valores centrales de la variable como su variabilidad, por lo que los gráficos de control se utilizan habitualmente en parejas: un gráfico para los valores medios (o los valores individuales si no tenemos grupos) y otro para la variabilidad.

Para el cálculo de los límites, debemos tener en cuenta que, si no disponemos de valores preespecificados fiables de la media y la desviación típica, debemos estimarlos a partir de muestras del proceso (subgrupos de tamaño \(n\)). No entraremos en este libro en los detalles teóricos de esta estimación, simplemente destacar que algunos gráficos de Shewhart utilizan la distribución de los rangos de muestras normales. A partir de esta distribución, se determinan unas constantes que dependen solo del tamaño de los grupos \(n\). El cálculo de los límites se realiza entonces mediante fórmulas en las que aparecen estas constantes. Tanto la tabla como las fórmulas se encuentran en el apéndice ??, y se pueden utilizar para construir los gráficos de control con Excel. No obstante, el software estadístico realiza estos cálculos automáticamente.

Como se vio en el apartado ??, para calcular los límites de control en Fase I podemos partir de valores pre-especificados de la media y la desviación típica, o bien estimar estos parámetros. En este punto es importante señalar que, si bien la media muestral \(\overline{x}\) es un buen estimador de la media poblacional \(\mu\), la desviación típica muestral \(s\) no es el mejor estimador de la desviación típica poblacional \(\sigma\). En su lugar, se utilizan los siguientes estimadores de la desviación típica:

\[\hat{\sigma}=\frac{s}{c_4};\qquad \hat{\sigma}=\frac{R}{d_2},\]

donde \(c_4\) y \(d_2\) son constantes que solo dependen del tamaño de la muestra \(n\) y \(R\) es el rango de la muestra. Las constantes están tabuladas y se pueden utilizar para realizar gráficos “a mano” o con Excel, aunque es muy costoso (el software estadístico lo hace automáticamente).

R

Para obtener gráficos de control con R utilizaremos básicamente el paquete qcc, y su función del mismo nombre. Esta función requiere siempre el tipo de gráfico a representar (uno de xbar, R, S, xbar.one, p, np, c, u, g) y los datos del proceso (de forma distinta según el tipo de gráfico). Las fases I y II se manejan pasando conjuntos de datos distintos (uno se usa para el cálculo de los límites, el otro no), o bien introduciendo los valores preespecificados de los parámetros. Existen más opciones disponibles, consulta la documentación del paquete. También se pueden añadir elementos y anotaciones al gráfico en la forma estándar.

Podemos guardar el resultado de la función qcc en un objeto de R. Por defecto, al guardar este objeto se muestra el gráfico en el dispositivo gráfico activo, esto se puede desactivar con el argumento plot. Este objeto lo podemos usar después para acceder a los datos del gráfico, generar el gráfico con la función plot, u obtener un resumen con la función summary. Si no se asigna la expresión a ningún objeto, se muestra en la salida de texto un resumen del objeto que se hubiera creado.

Excel

Realizar gráficos de control con Excel o cualquier otra hoja de cálculo es como hacerlo a mano. Debemos calcular los límites con las fórmulas en alguna celda, y después representarlos como una serie constante en un gráfico de dispersión. Los datos de cada subgrupo se pueden disponer por filas para calcular las medidas resumen en la siguiente columna a la última, y representar estas series como puntos y líneas en el gráfico de dispersión.

Minitab

En Minitab, los gráficos de control se encuentran en el menú Estadísticas/Herramientas de calidad. Están organizados por variables y atributos, aunque los cuadros de diálogo son muy similares. Podemos introducir los valores preespecificados de los parámetros en fase II.

14.1.2.1 Gráficos de la media y el rango

La pareja más famosa de gráficos de control son los de la media y el rango. Para realizar este tipo de gráficos debemos disponer de subgrupos racionales, idealmente del mismo tamaño. Para cada subgrupo se calculan la media y el rango, que serán los puntos a representar en ambos gráficos. El motivo de usar el rango como medida de la variabilidad cuando trabajamos con muestras pequeñas es que el rango es una medida más estable y fácil de calcular. Sin embargo, pierde efectividad a medida que aumenta el tamaño de muestra, siendo desaconsejable su uso para tamaños de muestra mayores de 10.

En el gráfico de la media, los puntos representan la media de cada subgrupo. Para fijar los límites, debemos considerar la distribución de probabilidad de dichas medias. Se cumple que las medias de muestras de tamaño \(n\) que provienen de una población cuya distribución es normal con media \(\mu\) y desviación típica \(\sigma\), siguen una distribución también normal con la misma media y desviación típica \(\frac{\sigma}{\sqrt{n}}\).

En el caso de que dispongamos de valores preestablecidos de la media y la desviación típica del proceso, \(\mu_0\) y \(\sigma_0\) respectivamente, las líneas del gráfico serán las siguientes:

\[\begin{align} LC &=& \mu_0,\\ LCI &=& \mu_0 - 3\frac{\sigma_0}{\sqrt{n}},\\ LCS &=& \mu_0 + 3\frac{\sigma_0}{\sqrt{n}}. \tag{14.1} \end{align}\]

En estas fórmulas podemos observar dos hechos importantes:

1. Si tenemos subgrupos de distintos tamaños, los límites de control no serán constantes, sino escalonados.
2. Se pueden simplificar los cálculos haciendo \(A = 3/\sqrt{n}\), siendo \(A\) una constante que solo depende del tamaño de subgrupo \(n\) y que se encuentra tabulada. Así, los límites de control quedarían: \(\mu_0 \pm A \sigma_0\).

Otro aspecto importante del gráfico de la media es que, aunque la distribución original de la variable no sea normal, el diseño del gráfico sigue siendo válido ya que las medias de cualquier distribución de probabilidad tienden a una distribución normal a medida que aumenta el tamaño de la muestra. Para distribuciones muy asimétricas, puede ser recomendable aumentar el tamaño de los subgrupos.

Si no tenemos unos valores pre-especificados de la media y la desviación típica, debemos estimarlos para calcular los límites. La media total la estimamos con la media de las medias de todos los subgrupos, \(\overline{\overline{X}}\), que será la línea central. Para estimar la desviación típica, y por tanto los límites de control, utilizamos el estimador que utiliza los rangos:

\[\frac{\overline{R}}{d_2 \sqrt{n}},\] donde \(\overline{R}=\frac{\sum\limits_{i=1}^n R_i}{n}\) es el rango medio de todas las muestras. Por tanto la línea central y los límites de control del gráfico de la media son los siguientes¹⁰⁸:

\[\begin{align} LC &= \overline{\overline{X}},\\ LCI &= \overline{\overline{X}} - \overline{R} \times \frac{3}{d_2 \sqrt{n}} = \overline{\overline{X}} - A_2 \overline{R},\\ LCS &= \overline{\overline{X}} + \overline{R} \times \frac{3}{d_2 \sqrt{n}} = \overline{\overline{X}} + A_2 \overline{R}.\\ \tag{14.2} \end{align}\]

Una fábrica produce placas metálicas cuyo espesor (thickness) es una característica crítica para la calidad. La fabricación se realiza en dos turnos cada día, y se toman seis muestras en cada turno. La tabla 14.1 muestra los 84 datos correspondientes a las muestras de una semana completa.

Tabla 14.1: Datos del espesor de placas metálicas

day	shift	p1	p2	p3	p4	p5	p6
1	1	0.713	0.776	0.743	0.713	0.747	0.753
1	2	0.749	0.726	0.774	0.744	0.718	0.677
2	1	0.778	0.802	0.798	0.793	0.801	0.798
2	2	0.780	0.729	0.793	0.777	0.774	0.742
3	1	0.775	0.735	0.749	0.737	0.701	0.727
3	2	0.727	0.736	0.768	0.759	0.734	0.731
4	1	0.748	0.748	0.778	0.789	0.764	0.792
4	2	0.778	0.750	0.777	0.736	0.807	0.822
5	1	0.752	0.738	0.788	0.740	0.754	0.741
5	2	0.726	0.745	0.705	0.770	0.744	0.784
6	1	0.775	0.742	0.735	0.768	0.752	0.762
6	2	0.763	0.749	0.750	0.759	0.787	0.729
7	1	0.793	0.757	0.775	0.772	0.750	0.797
7	2	0.796	0.784	0.807	0.780	0.731	0.750

R

Los datos se encuentran en el conjunto de datos ss.data.thickness2 del paquete SixSigma. A continuación se muestra el código que produce el gráfico de control de la figura 14.3.

Se utiliza el paquete qcc. La función qccGroups organiza los datos en una matriz donde cada fila tiene los datos de un subgrupo. Esta función requiere dos argumentos: el vector de datos (data) y el vector que contiene el identificador del subgrupo (sample), en este caso las columnas thickness y ushift del conjunto de datos ss.data.thickness2.

La función qcc crea el gráfico propiamente dicho. El gráfico más sencillo solo requiere la matriz de datos, y el tipo de gráfico. Se calculan así los límites con los datos de los 14 subgrupos (fase I sin valores preespecificados). Vemos que hay un punto fuera de los límites, aunque por poco. Habría que investigar y eliminar la causa asignable (o dejarlo, que es lo que hacemos aquí, porque no se encuentra una razón objetiva para eliminar el subgrupo).

Consulta la ayuda de las funciones correspondientes en RStudio para ver más opciones.

IMPORTANTE: En este material se utiliza la versión 3.0 del paquete qcc, que es posible no esté en CRAN en el momento de usar este material. Si es así, se puede instalar desde GitHub usando el paquete remotes de la siguiente forma:

remotes::install_github("luca-scr/qcc")

library(qcc, quietly = TRUE)
samples.thick <- qccGroups(
  data = ss.data.thickness2,
  x = thickness,
  sample = ushift)
gd_media <- qcc(data = samples.thick, 
                type = "xbar")  
plot(gd_media)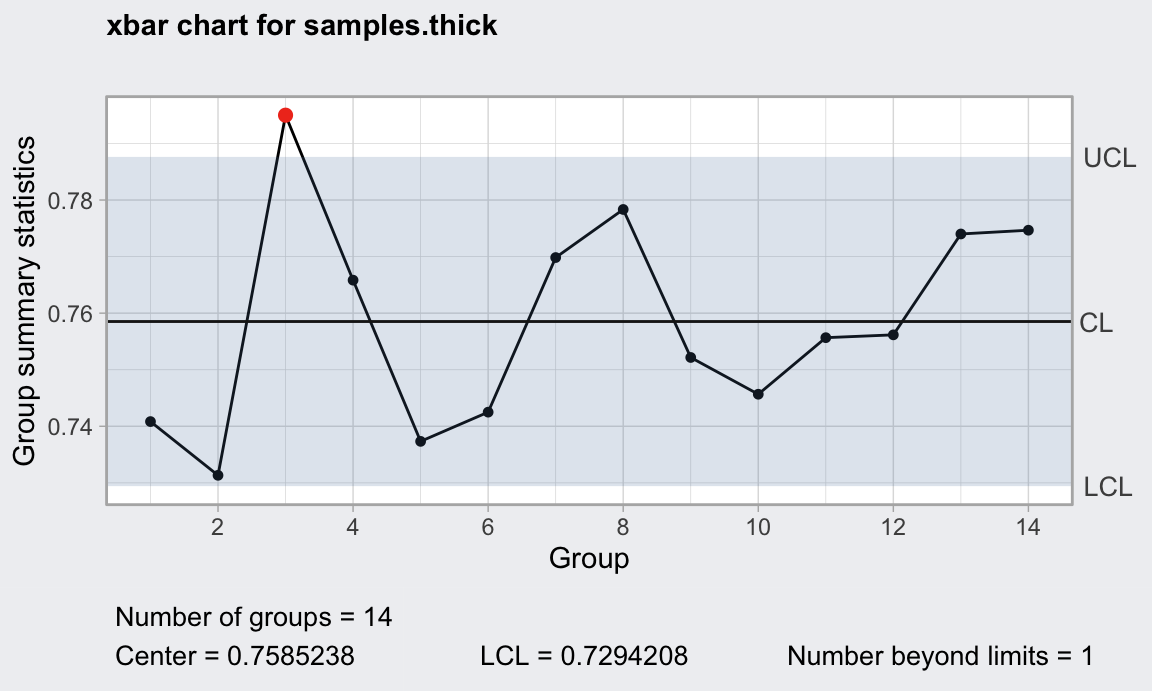

Figura 14.3: Gráfico de control de la media para el ejemplo del grosor de las placas metálicas

Excel

Para hacer el gráfico en Excel, debemos disponer los datos como en la tabla 14.1. Después, calcular las medias y rangos para cada subgrupo, la media global y el rango medio. A continuación crear series constantes para los límites de control y la línea central usando las fórmulas (14.2). Finalmente, representar gráficamente las cuatro series (líneas y datos) en un gráfico de dispersión, dando el formato adecuado a cada serie. Como se puede ver, mucho más laborioso. En el siguiente enlace se puede descargar un archivo Excel con este proceso realizado:

http://emilio.lcano.com/b/epac/datos/ejemplos_espesor2.xlsx

Minitab

Vamos al menú “Estadísticas > Gráficas de control > Gráficas de variables para subgrupos > Xbarra”. Debemos tener antes los datos en la hoja de trabajo, que se pueden importar desde Excel entre otros formatos. Indicar las columnas que tienen los datos, o el tamaño de los subgrupos, o la columna identifidadora (los datos pueden estar dispuestos apilados o extendidos).

En el gráfico del rango, los puntos representan el rango de cada subgrupo. Para calcular las líneas, partimos del estimador de la deviación típica:

\[\hat{\sigma}=\frac{R}{d_2} \implies R=d_2 \hat{\sigma},\] Nótese que el rango en este caso depende del tamaño del subgrupo a través de la constante \(d_2\). Por tanto, si tenemos distintos tamaños de subgrupos, la línea central del gráfico del rango será escalonada.

La desviación típica de los rangos viene dada por \(\sigma_R = d_3 \frac{R}{d_2}\) Si tenemos un valor pre-especificado \(\sigma_0\), los límites serían los siguientes:

\[LC = d_2 \sigma_0,\] \[LCI = d_2\sigma_0 - 3 d_3 \frac{d_2 \sigma_0}{d_2} = \sigma_0 (d_2 - 3d_3) = D_1 \sigma_0,\] \[LCS = d_2\sigma_0 + 3 d_3 \frac{d_2 \sigma_0}{d_2} = \sigma_0 (d_2 + 3d_3) = D_2 \sigma_0,\]

Cuando no disponemos de un valor pre-especificado \(\sigma_0\), utilizamos el estimador de la desviación típica \(\hat{\sigma}=\frac{R}{d_2}\), resultando en las siguientes líneas de control:

\[LC = \overline{R},\] \[LCI = \overline{R} - 3 d_3 \frac{\overline{R}}{d_2} = \overline{R} \left (1 - \frac{3d_3}{d_2}\right ) = D_3 \overline{R},\] \[LCS = \overline{R} + 3 d_3 \frac{\overline{R}}{d_2} = \overline{R} \left (1 + \frac{3d_3}{d_2}\right ) = D_4 \overline{R}.\] Recordemos que, para este gráfico, si tenemos tamaños de subgrupo distintos, el rango medio \(\overline{R}\) ha de calcularse para cada uno de los tamaños.

Para realizar el gráfico del rango de los datos de espesor procedemos de la misma forma en cualquiera de los tres programas, pero con la opción adecuada. En R, basta con cambiar el tipo de gráfico como se muestra a continuación, resultando en la figura 14.4. En Excel, de nuevo tendríamos que calcular las líneas de control y representar la serie de los rangos junto a ellas. En Minitab, seleccionaríamos en el menú el gráfico R.

r.thick <- qcc(data = samples.thick, type = "R")
plot(r.thick)

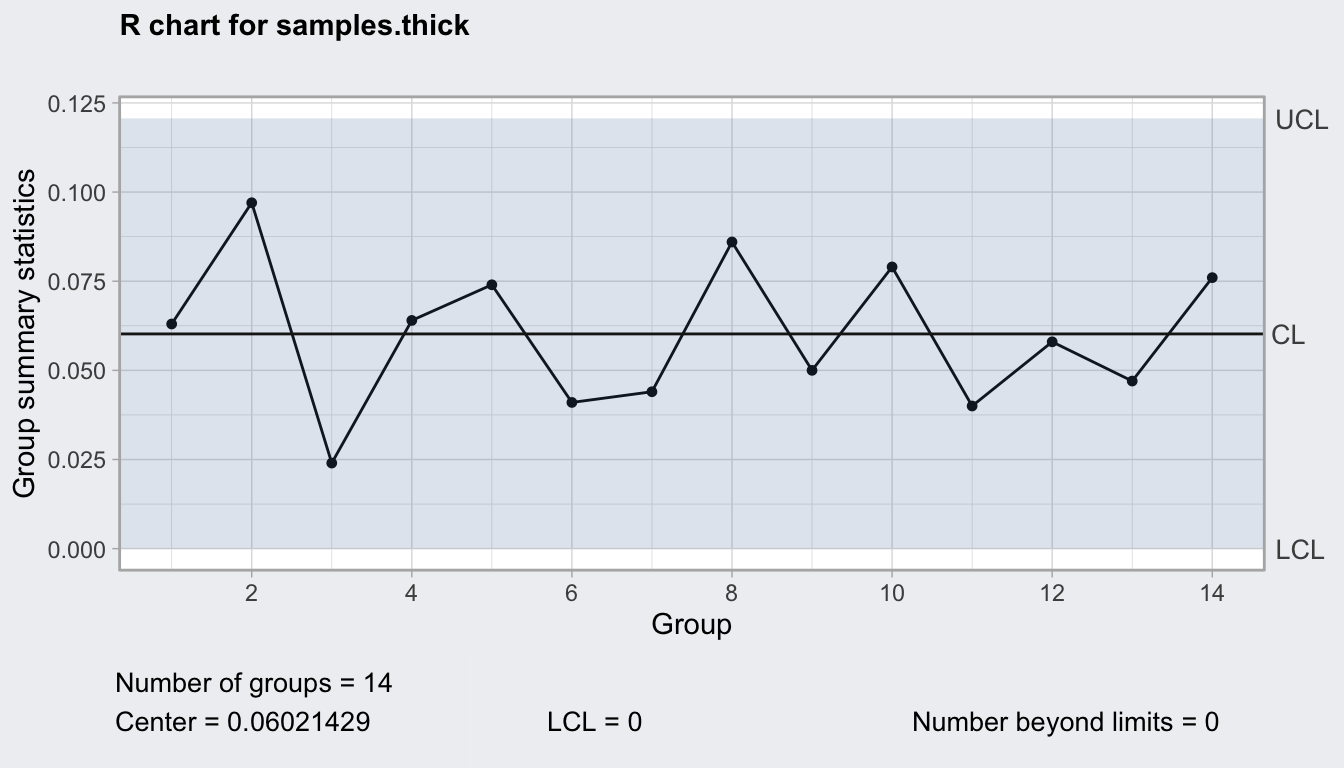
Figura 14.4: Gráfico del rango para el ejemplo del espesor

Un hecho importante a tener en cuenta es que al calcular los límites de control inferior en los gráficos de la variabilidad, las fórmulas pueden resultar en valores negativos. La variabilidad por definición siempre es positiva, por lo que en los casos en los que esto suceda, tomaremos el límite inferior igual a cero.

En este apartado hemos presentado primero el gráfico de la media y después el de los rangos por razones didácticas. Pero hay que tener en cuenta que antes de decidir si el proceso está bajo control con el gráfico de las medias, se debe comprobar que la variación también está controlada. Habitualmente, ambos gráficos se presentan conjuntamente, como veremos en el siguiente apartado.

14.1.2.2 Gráficos de la media y la desviación típica

Cuando el tamaño de los grupos es mayor de 10, no debemos utilizar el gráfico de los rangos, sino el de la desviación típica para controlar la variabilidad. En el gráfico de la desviación típica, los puntos representados son las desviaciones típicas muestrales \(s_i\) de cada subgrupo. Para estos gráficos utilizamos el estimador de la desviación típica del proceso que usa la desviación típica de las muestras en vez del rango:

\[\hat{\sigma} = \frac{\overline{s}}{c_4} \implies \overline{s}=c_4\hat{\sigma},\] donde \(c_4\) es una constante que solo depende del tamaño de subgrupo \(n\) y \(\overline{s}\) es el promedio de las desviaciones típicas de los \(k\) grupos. Necesitamos además estimar la desviación típica de las desviaciones típicas de los subgrupos, que es la siguiente:

\[\hat{\sigma_s} = \overline{s}\frac{\sqrt{1-c_4^2}}{c_4}.\]

Al igual que en el caso del rango, la desviación típica media debe calcularse para todos los tamaños de subgrupos existentes, pudiendo resultar en líneas de control escalonadas.

En el caso de que tengamos valores pre-especificados de la media y la desviación típica, \(\mu_0\) y \(\sigma_0\), el gráfico de control de la media se construye exactamente igual que se ha expuesto para los gráficos de la media y el rango. En este caso, las líneas de control del gráfico de las desviaciones típicas se calculan así:

\[LC = c_4\sigma_0,\]

\[LCI = c_4\sigma_0 - 3 c_4\sigma_0\frac{\sqrt{1-c_4^2}}{c_4} = \sigma_0 \left(c_4 - 3\sqrt{1-c_4^2} \right) = B_5\sigma_0,\] \[LCS = c_4\sigma_0 + 3 c_4\sigma_0\frac{\sqrt{1-c_4^2}}{c_4} = \sigma_0 \left(c_4 + 3\sqrt{1-c_4^2} \right) = B_6\sigma_0.\]

Si no tenemos valores preestablecidos, el cálculo de los límites del gráfico de la media lo realizamos estimando la desviación típica del proceso a partir de las desviaciones típicas de los subgrupos, de manera que las líneas de control del gráfico de control de la media quedan:

\[LC = \overline{\overline{X}},\] \[LCI = \overline{\overline{X}} - 3 \times \frac{\overline{s}}{c_4 \sqrt{n}} = \overline{\overline{X}} - A_3 \overline{s},\] \[LCS = \overline{\overline{X}} + 3 \times \frac{\overline{s}}{c_4 \sqrt{n}} = \overline{\overline{X}} + A_3 \overline{s}.\]

Las líneas de control del gráfico de las desviaciones típicas cuando no tenemos un valor preestablecido \(\sigma_0\) quedan así.

\[LC = \overline{s},\]

\[LCI = \overline{s} - 3 \overline{s}\frac{\sqrt{1-c_4^2}}{c_4} = \overline{s} \left(1 - \frac{3\sqrt{1-c_4^2}}{c_4} \right) = B_3\overline{s},\] \[LCS = \overline{s} + 3 \overline{s}\frac{\sqrt{1-c_4^2}}{c_4} = \overline{s} \left(1 + \frac{3\sqrt{1-c_4^2}}{c_4} \right) = B_4\overline{s}.\]

Vamos a completar el ejemplo anterior ilustrando las fases I y II. Hagamos dos salvedades. Por una parte, en este conjunto de datos tenemos 14 subgrupos, pero lo ideal sería tener entre 25 y 30. Por otra parte, podríamos seguir utilizando el gráfico del rango ya que el tamaño de los subgrupos es menor de 10.

Supongamos que del estudio anterior se ha llegado a la conclusión de que se pueden tomar como valores preespecificados una media \(\mu_0=0.76\) y una desviación típica \(\sigma_0=0.025\). Entonces podemos fijar los límites tomando estos valores (ya sea en las fórmulas a mano, o en el software). Además, se han tomado datos de un nuevo subgrupo, resultando en las siguientes mediciones: \(0.719, 0.759, 0.708, 0.83, 0.766, 0.709\). Entonces representamos las medidas resumen de esta nueva muestra frente a los límites fijados en fase I.

El siguiente código produce el gráfico de la figura 14.5 con R. Nótese cómo añadimos a las funciones los argumentos para los valores preespecificados y los nuevos datos. En Excel, podemos ir añadiendo los nuevos datos a la hoja de cálculo y extendiendo las series, pero hay que tener mucho cuidado con la definición de las fórmulas. En Minitab, en el cuadro de diálogo de los gráficos vamos a las opciones del gráfico y los introducimos en la pestaña “Parámetros”.

En este caso vemos que, aunque el valor medio de la muestra está dentro de los límites, la desviación típica no, y tendríamos que buscar la causa asignable de esta situación fuera de control.

new.sample <- matrix(c(0.719, 0.759, 0.708, 0.83, 0.766, 0.709),
                     ncol = 6)
ccxbar <- qcc(data = samples.thick, type = "xbar",
              center = 0.76,  std.dev = 0.025,
              newdata = new.sample, newlabels = "8.1",
              plot = FALSE)

ccs <- qcc(data = samples.thick, type = "S",
           newdata = new.sample, newlabels = "8.1",
           plot = FALSE)
library(ggplotify)
library(gridExtra)
grid.arrange(
  plot(ccxbar, restore.par = FALSE, add.stats = FALSE),
  plot(ccs, add.stats = FALSE)
)

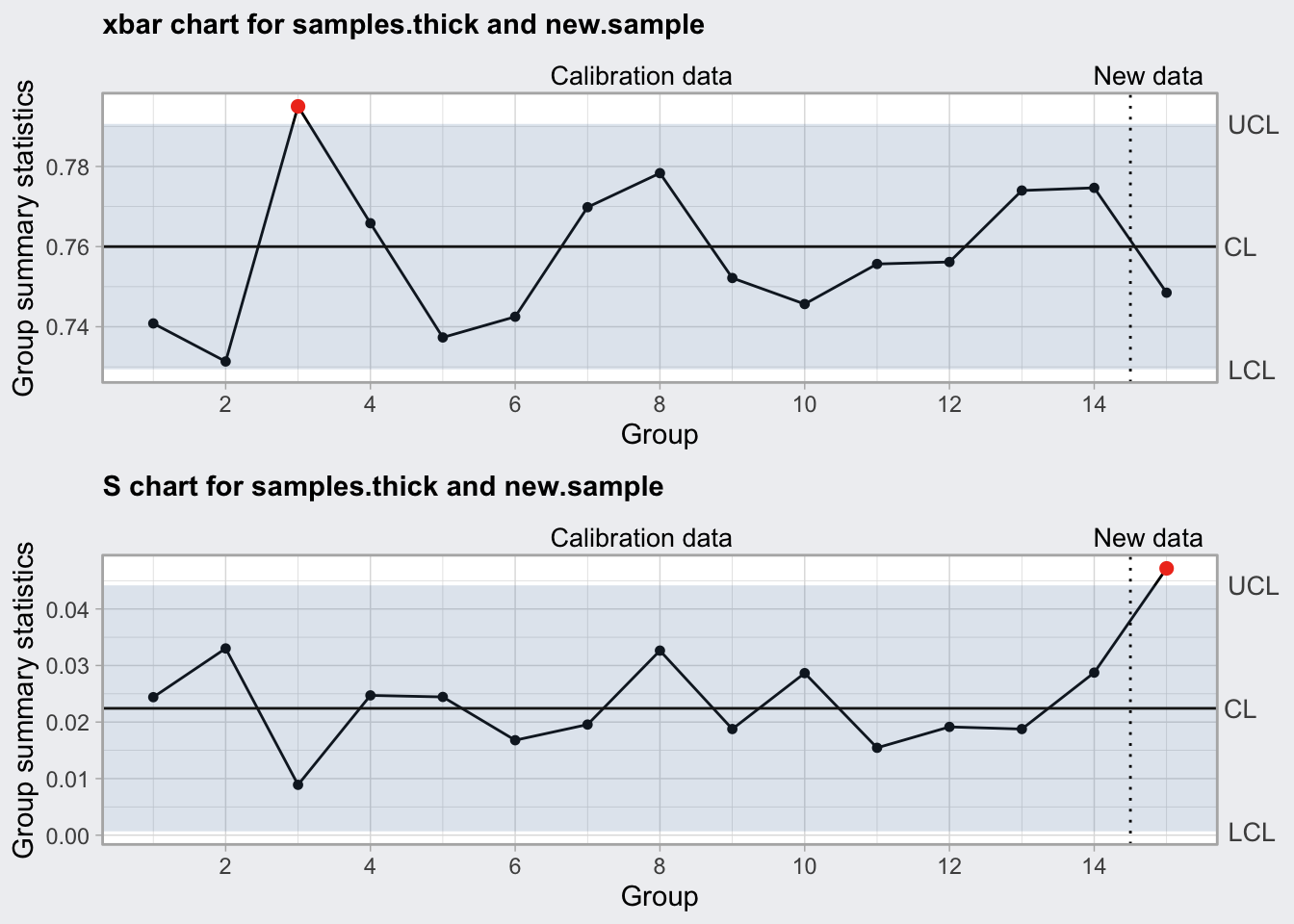
Figura 14.5: Gráfico de la media y la desviación típica monitorizando nuevos datos

14.1.2.3 Gráficos de valores individuales y rangos móviles

Cuando no podemos crear grupos racionales, podemos analizar los datos individualmente. En realidad lo que estamos haciendo es partir de la base de que cada dos observaciones son un grupo, y así tenemos un rango móvil que es la diferencia entre cada dos valores consecutivos. De esta forma se pueden aplicar los principios de Shewhart para tamaños de muestra \(n=2\). La desviación típica a tener en cuenta no va a ser la de valores medios, sino la propia del proceso. Así, cuando tenemos valores preestablecidos \(\mu_0\) y \(\sigma_0\), las líneas de control del gráfico de valores individuales son las siguientes:

\[LC=\mu_0,\] \[LCI=\mu_0 - 3\sigma_0,\] \[LCS=\mu_0 + 3\sigma_0.\] Si no disponemos de valores pre-especificados, entonces estimamos la desviación típica a partir del rango móvil como:

\[\hat{\sigma} = \frac{\overline{R}_m}{d_2},\] donde \(d_2\) se toma para \(n=2\), es decir, \(1.228\), y \(\overline{R}_m\) es el promedio de los rangos móviles:

\[\overline{R_m}=\frac{\sum_{i=1}^{k-1} R_{m_i}}{k-1}; \; R_{m_i}=|X_{i+1}-X_i|.\] Entonces las líneas de control del gráfico de los valores individuales quedaría:

\[LC=\overline{X},\] \[LCI=\overline{X} - 3\frac{\overline{R}_m}{d_2}= \overline{X} - 2.660 \overline{R}_m,\] \[LCI=\overline{X} + 3\frac{\overline{R}_m}{d_2}= \overline{X} + 2.660 \overline{R}_m.\]

Previamente a controlar los valores individuales, debemos controlar la variabilidad. Para ello utilizamos el gráfico de los rangos móviles, utilizando las fórmulas para subgrupos de tamaño \(n=2\). Si tenemos un valor preestablecido de la desviación típica, las líneas de control serán las siguientes:

\[LC = d_2 \sigma_0 = 1.128 \sigma_0,\] \[LCI = d_2\sigma_0 - 3 d_3 \frac{d_2 \sigma_0}{d_2} = \sigma_0 (d_2 - 3d_3) \leadsto 0,\] \[LCS = d_2\sigma_0 + 3 d_3 \frac{d_2 \sigma_0}{d_2} = \sigma_0 (d_2 + 3d_3) = D_2 \sigma_0 = 3.686\sigma_0.\]

Si no tenemos un valor pre-especificado de la desviación típica, las líneas de control del gráfico de los rangos móviles son las siguientes:

\[LC = \overline{R}_m,\] \[LCI = \overline{R}_m - 3 d_3 \frac{\overline{R}_m}{d_2} = \overline{R}_m \left (1 - \frac{3d_3}{d_2}\right ) \leadsto 0,\] \[LCS = \overline{R}_m + 3 d_3 \frac{\overline{R}_m}{d_2} = \overline{R}_m \left (1 + \frac{3d_3}{d_2}\right ) = D_4 \overline{R}_m = 3.267 \overline{R}_m.\]

A modo ilustrativo, tomamos las primeras 24 observaciones de los datos del ejemplo anterior (tabla 14.1). Para crear el gráfico de las medias móviles en R, tenemos que “simular” las muestras de tamaño 2. El siguiente código crea los gráficos de la figura 14.6.

En Minitab, seleccionamos los gráficos para datos no agrupados. En Excel tendríamos que crear las series de rangos móviles, calcular los límites y representar las series como en el apartado anterior.

thickness2days <- ss.data.thickness2$thickness[1:24]
mov.samples <- cbind(thickness2days[1:23], 
    thickness2days[2:24])
cci <- qcc(thickness2days, type = "xbar.one", plot = FALSE)
ccmr <- qcc(mov.samples, type = "R", plot = FALSE)
grid.arrange(
  plot(cci, add.stats = FALSE),
  plot(ccmr, add.stats = FALSE)
)

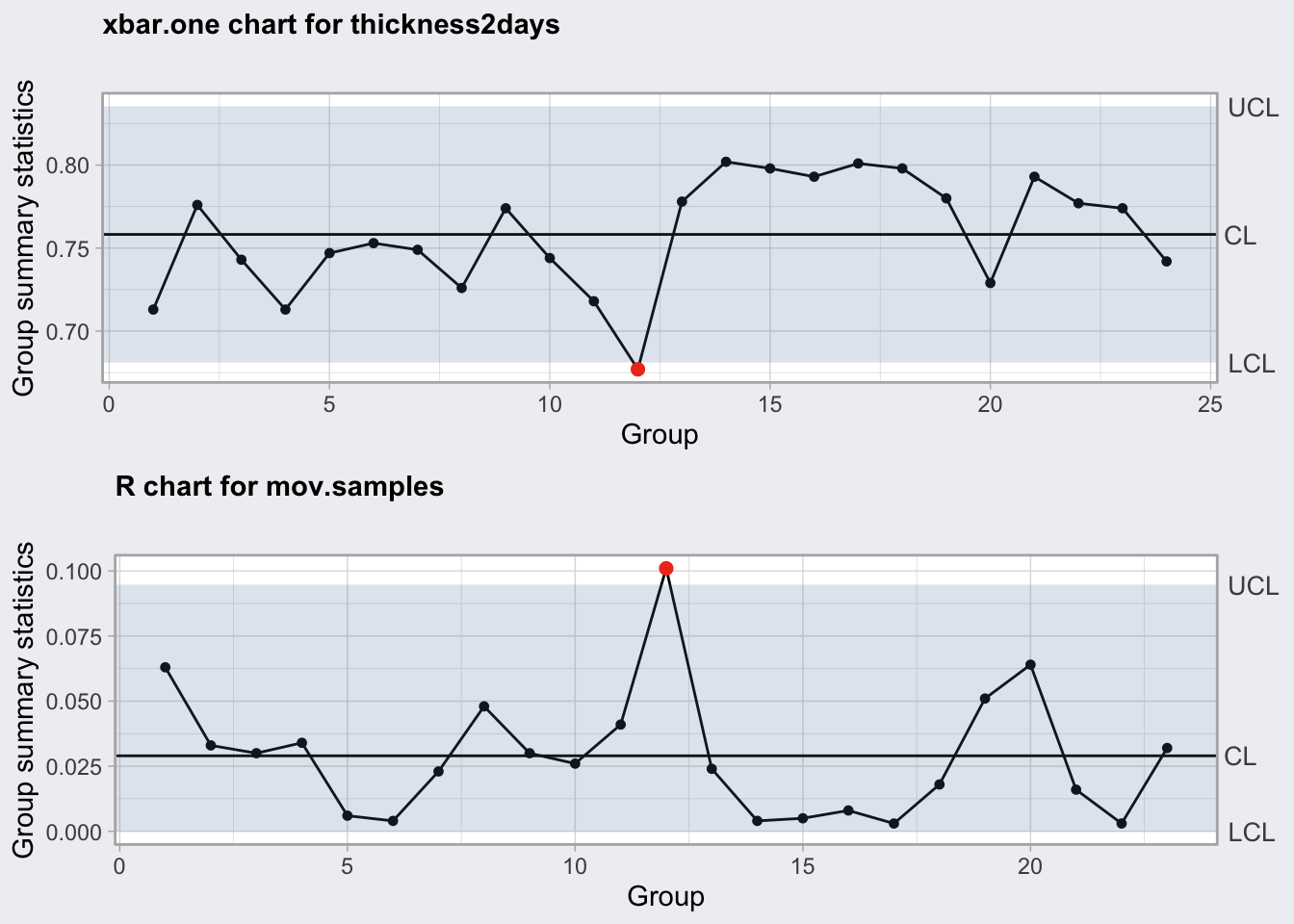
Figura 14.6: Gráficos de valores individuales y media móvil

14.1.2.4 Tamaño de la muestra

Como se explica en el capítulo ??, utilizamos muestras para hacer inferencia sobre nuestra población. Por ejemplo, la medición del proceso en un día determinado (muestra), para sacar conclusiones sobre el desempeño del proceso a largo plazo (población). Sin entrar en los detalles teóricos ni de formulación, se proporcionan aquí algunos conceptos referentes al muestreo que pueden aparecer al aplicar el Control Estadístico de Procesos.

Al utilizar gráficos de control, lo que estamos haciendo son sucesivos contrastes de hipótesis para comprobar si el proceso está fuera de control. Así, para cada punto que representamos, realizamos el siguiente contraste:

H\(_0\): El proceso está bajo control

H\(_1\): El proceso está fuera de control

donde \(H_0\) es lo que llamamos la hipótesis nula, y \(H_1\) es la hipótesis alternativa, que es lo que nos interesa demostrar, porque requerirá una acción.

Al fijar los límites de control en tres desviaciones típicas más allá de la media, estamos fijando el nivel de significación \(\alpha\) para estos contrastes de hipótesis en 0.0027. Cuando un punto está fuera de los límites, entonces rechazamos la hipótesis de que el proceso está bajo control, y decimos que el proceso está fuera de control (de hecho con una confianza superior al 99.73%). El tamaño de la muestra \(n\) está directamente relacionado con:

• El nivel de significación \(\alpha\), que es la probabilidad de que la muestra caiga fuera de los límites estando el proceso bajo control (error tipo I).
• La potencia del contraste \(1-\beta\), siendo \(\beta\) la probabilidad de que la muestra caiga dentro de los límites, estando el proceso fuera de control (error tipo II).
• El máximo error cometido al estimar el parámetro, \(\delta\).

La desviación con respecto al verdadero valor del parámetro a estimar, en este caso la media, se puede dar en valor absoluto (\(\delta\)), en cuyo caso necesitamos conocer la desviación típica de los datos para calcular el tamaño de la muestra, o como número de desviaciones típicas, es decir, \(\delta=k\sigma\). En este caso, los cuatro valores anteriores están relacionados de forma que conociendo tres de ellos, el otro queda determinado. Por tanto, si fijamos el nivel de significación, potencia del test, y tamaño de la muestra, podemos saber cuál es la desviación que vamos a detectar en nuestro proceso \(\delta\). O bien, podemos fijar el máximo error que estamos dispuestos a cometer y obtener el tamaño de muestra que necesitamos, y así sucesivamente.

A la hora de decidir el tamaño de los subgrupos, no existe una regla de oro que sirva para todos los procesos. Esta decisión se tomará en base a las características del proceso y de la empresa. En algunos casos el número de muestras que podemos tomar está limitado por un determinado presupuesto. Entonces, para el mismo tamaño total de muestra se puede decidir entre tomar muchas muestras de tamaño pequeño, o menos muestras de tamaño más grande. En general se prefieren muestras más frecuentes de tamaño menor para detectar el cambio más rápido, pero esto depende de las características del proceso.

En la elección final de tamaño de los subgrupos, se tendrá en cuenta, además del coste de muestreo, la potencia del test que deseamos, y el cambio mínimo que queremos detectar.

El diseño final del gráfico de control y su plan de muestreo, se basará en la magnitud del cambio que queremos detectar. Vamos a estudiar el tamaño de los subgrupos para el gráfico de la media. Un desplazamiento en la media del proceso, producirá un efecto en el gráfico de control como se muestra en la figura 14.7. Vemos una situación típica en la que un proceso está bajo control (azul) y a partir de un determinado momento, se produce un desplazamiento en la media, que producirá puntos fuera de los límites, en este ejemplo en el segundo punto. Los demás estarían dentro de los límites de control (error de tipo II).

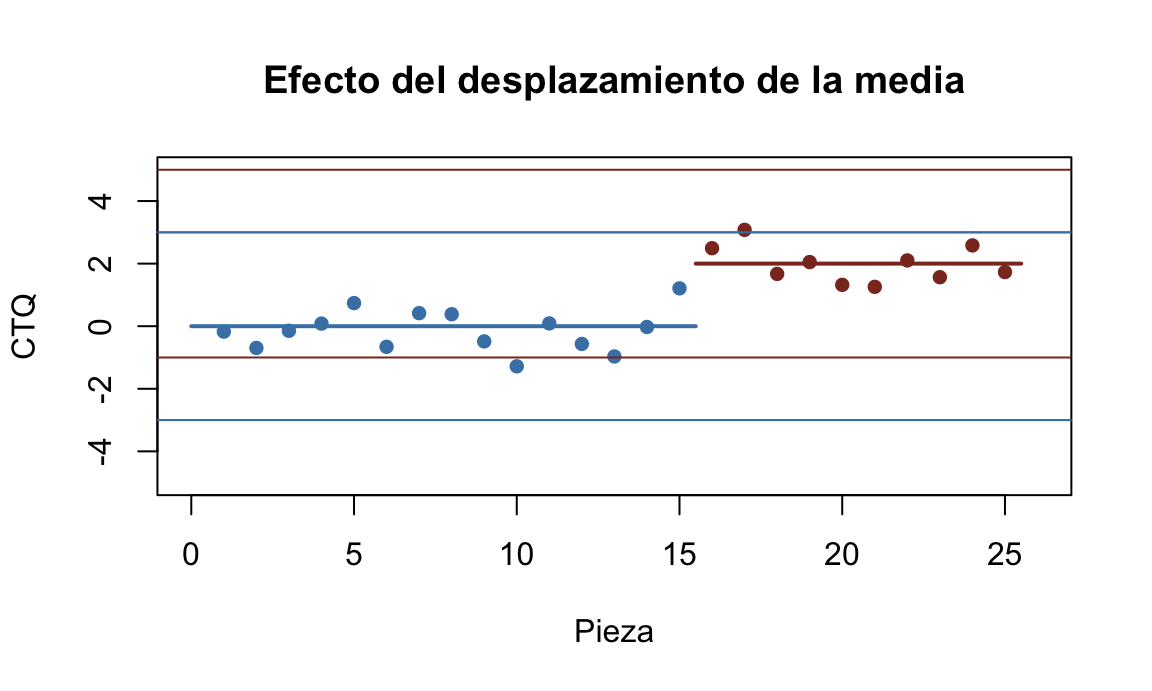
Figura 14.7: Efecto del desplazamiento de la media en el gráfico de control

Dada la distribución de las medias de tamaño \(n\), la probabilidad de no detectar un desplazamiento de \(k\) desviaciones típicas desde la media, es decir:

\[\beta = P\{ \mathit{LCI} \leq \bar{x} \leq \mathit{LCS} \, |\, \mu = \mu_0 + k\sigma \},\] la podemos calcular de la siguiente forma:¹⁰⁹

\[\beta = Z(3-k\sqrt{n}) - Z(-3-k\sqrt{n}),\] donde \(Z\) es la función de distribución normal estándar (\(\mu=0,\, \sigma = 1\)). Por ejemplo, en el anterior gráfico de control, la media a partir de cierto momento (puntos rojos) se ha desplazado dos desviaciones típicas por encima de la media bajo control (puntos azules). ¿Cuál es la probabilidad de no detectar este cambio, es decir, \(\beta\)? Supongamos que cada punto representa la media de un grupo de tamaño \(n=5\). Entonces:

\[\beta = Z(3-2\cdot\sqrt{5}) - Z(-3-2\cdot\sqrt{5}) = Z(-1.47) - Z(-7.47)=0.07\] Por tanto podemos calcular el valor \(\beta\) para distintos valores de \(n\) y \(k\), y representar estos valores gráficamente como veremos a continuación.

Una herramienta gráfica muy útil para decidir tamaños de muestra son las curvas características de operación (OC Curves). Estas curvas representan, para varios tamaños de muestra determinados (típicamente entre 1 y 25), la desviación que se detectará, que puede estar expresada en términos absolutos, \(\delta = k \sigma\), o en número de desviaciones típicas, \(\sigma\) frente a la probabilidad de error de tipo II \(\beta\), es decir, probabilidad de que el proceso esté fuera de control pero dentro de los límites, fijado un error de tipo I \(\alpha\), es decir, probabilidad de que el proceso esté bajo control pero se salga de los límites. El error tipo I viene determinado por las 3 desviaciones típicas desde la media que marcan los límites de control, es decir 0.0027.

El error tipo II, \(\beta\), se interpreta también de la siguiente forma: En el caso de que la media del proceso se desplace \(k\) desviaciones típicas, \(\beta\) es la probabilidad de no detectar dicho cambio. Podemos ver en la figura 14.8 que el gráfico de control de la media es muy potente para detectar cambios importantes, pero no tanto para detectar cambios más pequeños.

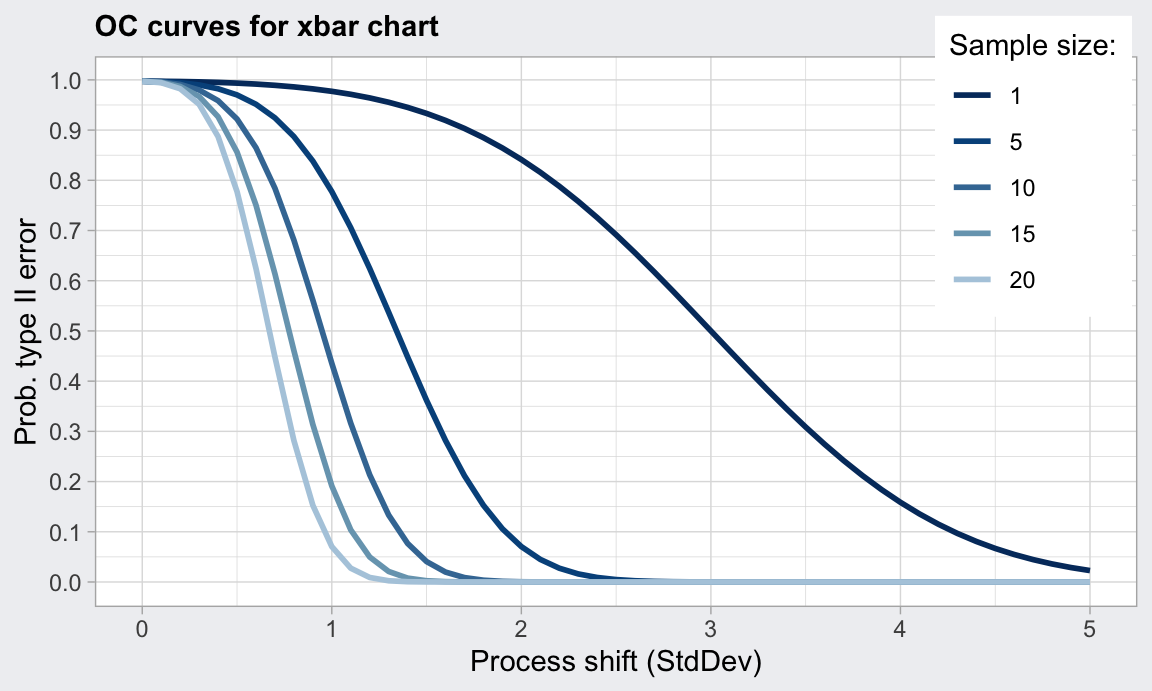
Figura 14.8: curva de operación característica para el gráfico de la media y varios valores de \(n\)

Otro dato a tener en cuenta para determinar el tamaño y la frecuencia del muestreo es la longitud media de racha (Average Run Length, ARL). El ARL es el número de muestras, en promedio, que se tomarán antes de detectar un cambio en la muestra. Esta variable aleatoria se corresponde con una distribución Geométrica de parámetro \(p\), cuya esperanza es \(1/p\). Por tanto, el tamaño medio de racha se calcula como el inverso de la probabilidad de que una muestra esté fuera de los límites. En el caso de los gráficos de control cuyos límites se fijan en 3 desviaciones típicas, incluso cuando el proceso está bajo control en promedio tendremos valores fuera de los límites aproximadamente cada 370 muestras:

\[\mathit{ARL}=\frac{1}{p}= \frac{1}{0.0027}=370.37.\]

Ahora bien, lo que nos interesa es saber detectaremos un cambio en la media como el descrito en la curva OC. El valor de \(\beta\) nos indica la probabilidad de no detectar este cambio en la primera muestra. La probabilidad de detectar el cambio en la primera muestra será \(1-\beta\), también conocido como potencia del gráfico. En general, para un plan de muestreo con un \(\beta\) determinado, el número de muestras necesarias para detectar el cambio será:

\[\mathit{ARL} = \frac{1}{1-\beta}.\]

Por ejemplo, para \(k=1\) y \(n=5\), \(\beta=0.25\). Entonces:

\[\mathit{ARL} = \frac{1}{1-0.25}=4,\]

lo que quiere decir que necesitaremos 4 muestras en promedio para detectar el cambio. Dependiendo del número de unidades producidas, se puede fijar la frecuencia del muestreo en función del tiempo que estamos dispuestos a esperar hasta detectar una desviación en el proceso. Es decir, si queremos detectar un cambio en la media de una magnitud determinada, por ejemplo en el mismo día que se produce, analizamos la producción diaria y buscamos el ARL que nos interesa. En el ejemplo anterior, si tomamos muestras cada hora, entonces en promedio estaríamos detectando un cambio en la media en una desviación típica cada cuatro horas. Otro ejemplo: si nuestra producción es de 1000 lotes y tomamos muestras de los lotes, entonces tendríamos que muestrear 4 lotes cada día si queremos detectar el cambio (en promedio) en el mismo día, es decir, uno de cada 250. Si tenemos turnos de 24 horas, tendríamos que tomar una muestra cada 6 horas.

Las fórmulas vistas en esta sección se refieren al gráfico de control de la media. Existen también métodos para el resto de gráficos, aunque no son tan claros y efectivos con los vistos aquí, consulta la bibliografía. Algunas aplicaciones permiten la generación de curvas OC para distintos gráficos de control.

14.1.3 Gráficos de control por atributos

No siempre podemos medir las características de calidad numéricamente. Sin embargo, es sencillo hacer comprobaciones sobre ciertos atributos, por ejemplo conforme/no conforme. Podemos realizar control de procesos sobre estos datos mediante los gráficos de control por atributos. Al igual que con los gráficos por variables, en este tipo de gráficos se detectan situaciones altamente improbables según la distribución de probabilidad subyacente en el proceso. En este caso, en vez de utilizar la distribución normal se utilizan distribuciones de probabilidad discretas como la binomial y la de Poisson. Estas distribuciones quedan determinadas por un único parámetro para calcular la media y la desviación típica, por lo que solamente se utiliza un gráfico para controlar el proceso. Salvo por esta dferencia, la mecánica de los gráficos de control por atributos es idéntica a la de los gráficos de control por variables. Los límites de control se deben fijar en una primera fase, bien porque tenemos unos valores estándar dados de los parámetros, o porque los estimamos con una muestra preliminar. Después, en la fase II se controlan los nuevos valores con estos límites en busca de causas de variación asignables.

14.1.3.1 Gráficos \(p\) y \(np\)

El gráfico \(p\) Se utiliza para controlar proporciones dentro de subgrupos con un tamaño determinado, por ejemplo lotes, pedidos en un día, etc. Así, los puntos representados en el gráfico para cada subgrupo son las proporciones de elementos que tienen un determinado atributo. Así, si un subgrupo tiene tamaño \(n_j\) y hay \(D_j\) elementos que presentan el atributo, el punto a representar es:

\[p_j = \frac{D_j}{n_j}.\] Si disponemos de un valor estándar para la proporción de elementos de nuestro proceso que tienen el atributo, \(p_0\), entonces las líneas de control del gráfico \(p\) son las siguientes:

\[LC = p_0.\] \[LCI = p_0 - 3 \sqrt{p_0(1-p_0)/n},\] \[LCS = p_0 + 3 \sqrt{p_0(1-p_0)/n},\]

Si por el contrario no disponemos de un valor estándar de \(p\), tenemos que estimarlo con una muestra perliminar mediante el porcentaje global \(\overline{p}\):

\[\bar{p}=\frac{\sum_{j=1}^m D_j}{\sum_{j=1}^m n_j}.\]

El gráfico de control \(np\) se utiliza para controlar el número de elementos con la característica a controlar, no la proporción, pero para el mismo tipo de datos, es decir, cuando tenemos grupos con un determinado tamaño. Además, este tamaño debe ser el mismo en todos los grupos. En este caso el valor a representar es \(D_j\), y los límites de control son los siguientes:

\[LC = n\bar{p},\]

\[LCS = n\bar{p} + 3 \sqrt{n\bar{p}(1-\bar{p})},\]

\[LCI = n\bar{p} - 3 \sqrt{n\bar{p}(1-\bar{p})},\]

sustituyendo \(\overline{p}\) por \(p_0\) cuando disponemos de este valor estándar.

Para representar gráficos de control por atributos con R, además del vector con los datos del proceso, por ejemplo número de defectuosos, o número de defectos, es necesario proporcionarle los tamaños de los grupos o las muestras mediante el argumento sizes (excepto para el gráfico \(c\)).

Supongamos que queremos monitorizar la proporción de piezas cuyo grosor excede \(0.775\) en cada turno. El siguiente código crealos datos adecuados y crea el gráfico \(p\) de la figura 14.9. El gráfico \(np\) para estos mismos datos se obtendría simplemente cambiado el tipo de gráfico.

En Excel tendríamos que calcular las proporciones de cada muestra y representar esta serie frente a los límites de control calculados con los datos o con un valor preespecificado de \(p\). Cuando los tamaños de muestra son siempre iguales es sencillo, pero si tenemos distintos tamaños de muestra, hacer un gráfico con límites escalonados en Excel se complica.

En Minitab, seleccinamos los gráficos de control por atributos y proporcionamos la información de qué columnas contienen los recuentos y los tamaños de muestra (o un número si es fijo).

thick.attribute <- aggregate(thickness ~ ushift, 
    data = ss.data.thickness2,
    FUN = function(x){
      sum(x>0.775)
    })
thick.p <- qcc(data = thick.attribute$thickness,
    type = "p",
    sizes = 6)
plot(thick.p)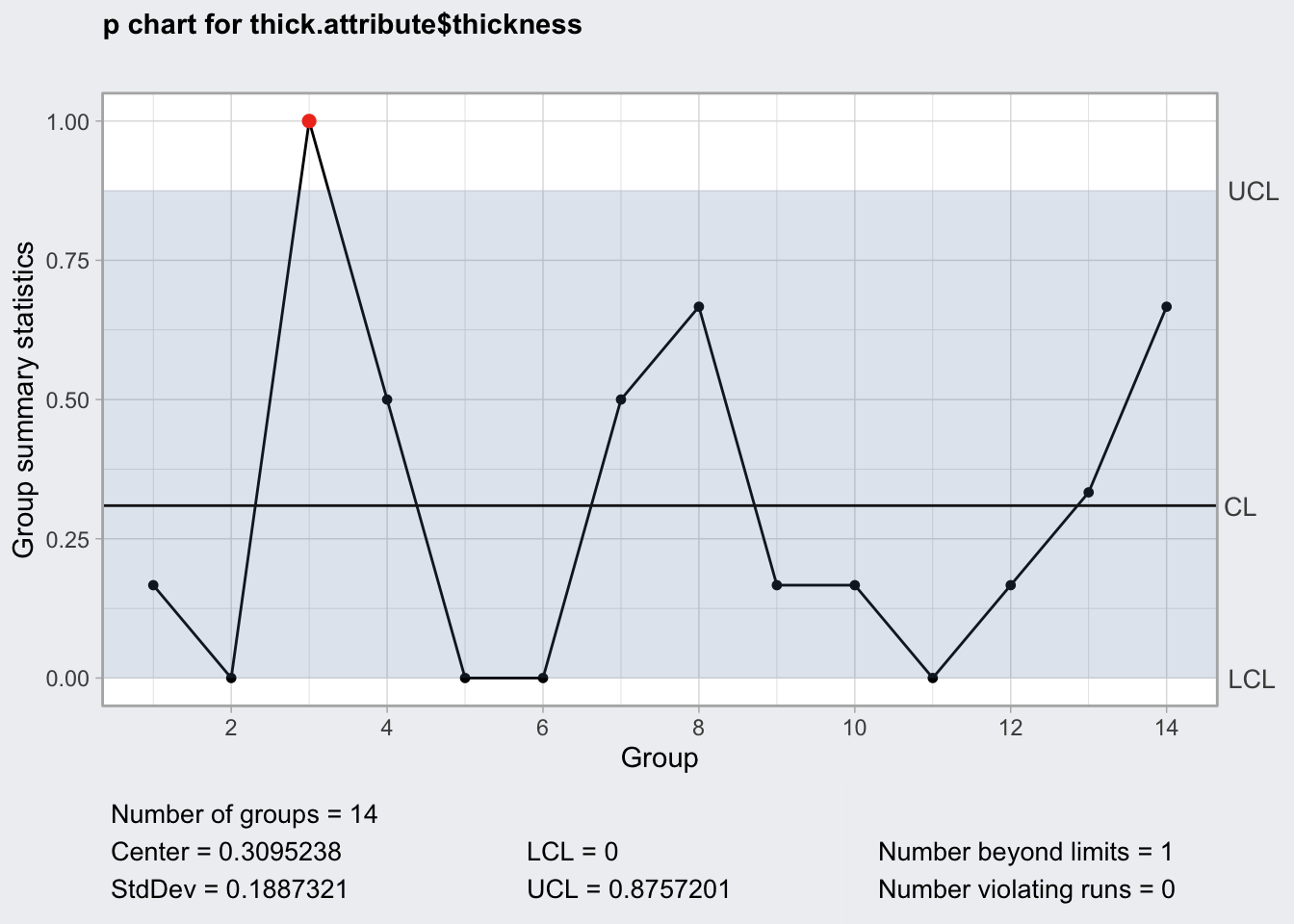

Figura 14.9: Gráfico p de proporción piezas espesor mayor de 0.775

14.1.3.2 Gráficos \(c\) y \(u\)

El gráfico de control \(c\) se utiliza para controlar el número total de eventos en un determinado proceso en soporte continuo, es decir, errores por unidad, que siguen una distribución de Poisson teóricamente con infinitos valores posibles, es decir, no hay un tamaño de grupo para calcular proporciones como en el caso anterior. El uso más habitual es para monitorizar el número total de no conformidades medidas en una serie de \(m\) muestras del mismo tamaño, bien sean intervalos temporales o espaciales. Por ejemplo, el número de llamadas no atendidas por hora, número de no conformidades por día, número de manchas por \(m^2\), etc. Así, los puntos representados en el gráfico de control será el recuento \(c_j\) de esos eventos.

La distribución de Poisson solamente depende de un parámetro que es el número medio de eventos por unidad. Por tanto, si tenemos un valor estándar para este número medio de eventos por unidad \(c_0\), las líneas de control serán:

\[LC = c_0,\]

\[LCI = c_0 - 3 \sqrt{c_0},\]

\[LCS = c_0 + 3 \sqrt{c_0},\]

Cuando no disponemos de un valor estándar para el promedio de eventos, lo estimamos con \(m\) muestras preliminares como:

\[\overline{c} = \frac{\sum\limits_{j=1}^{m}{c_j}}{m},\]

donde \(c_j\) es el número total de defectos en la muestra j-ésima y \(m\) es el número de muestras (horas, \(m^2\), etc.).

En el conjunto de datos que venimos utilizando, se inspeccionan aleatoriamente algunas placas (1, 2, o 3) y se cuenta el número de defectos en cada pieza. El gráfico \(c\) representaría esos recuentos en cada pieza. El siguiente código de R produce la figura 14.10.

En Excel bastaría con representar la serie de recuentos frente a los límites calculados con las fórmulas.

En Minitab, seleccionamos el gráfico \(c\) dentro de los gráficos de control por atributos e indicamos qué columna de la hoja de trabajo contiene los recuentos.

flaws <- ss.data.thickness2$flaws[
    !is.na(ss.data.thickness2$flaws)]
thick.c <- qcc(data = flaws, type = "c")
plot(thick.c)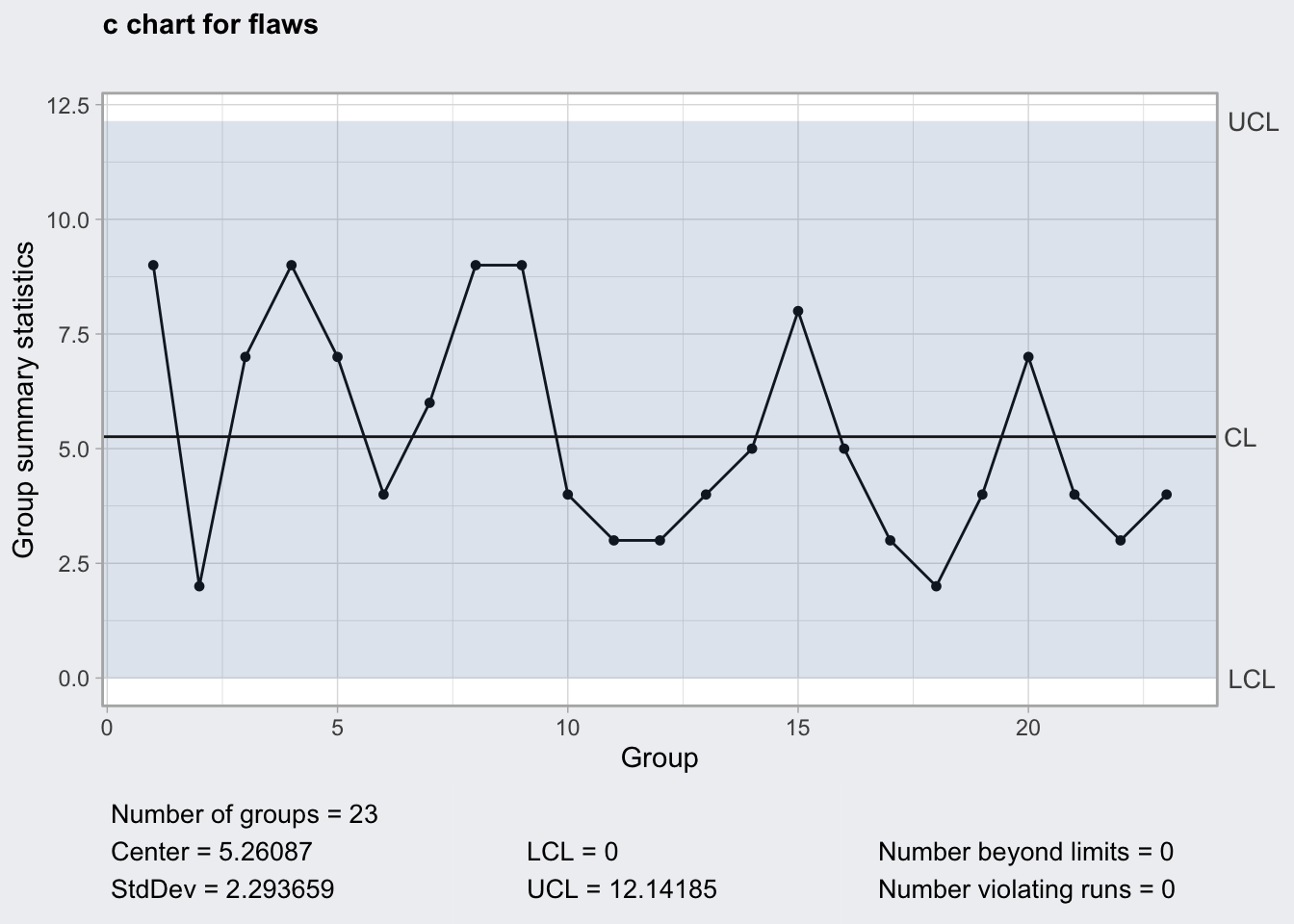

Figura 14.10: Gráfico c de los defectos

En ocasiones, los recuentos se realizan en una serie de muestras de tamaño \(n_j\) contabilizando el número total de eventos. Entonces nos puede interesar monitorizar el número medio de eventos por unidad:

\[u_j = \frac{c_j}{n_j},\] y lo hacemos mediante el gráfico \(u\), cuyas líneas de control son las siguientes cuando no tenemos un valor estándar \(u_0\):

\[LC = \bar{u} = \frac{\sum\limits_{j=1}^m u_j}{\sum\limits_{j=1}^mn_j},\]

\[LCI_i = \bar{u} - 3 \sqrt{\frac{\bar{u}}{n_j}},\] \[LCS_i = \bar{u} + 3 \sqrt{\frac{\bar{u}}{n_j}}.\]

Si disponemos de un valor estándar del número de defectos por unidad \(u_0\) lo utilizamos en las fórmulas en vez de \(\overline{u}\).

El siguiente código de R produce el gráfico de la figura 14.11. Nótese que primero transformamos los datos, pero si ya tenemos un conjunto de datos con las columnas de número de inspeccionadas y número de defectos total, no haría falta nada más.

En Excel, si el número de piezas inspeccionadas es constante el gráfico es fácil de construir. Pero si los tamaños no son constantes como en este caso, el gráfico puede ser confuso.

En Minitab, elegimos el gráfico \(u\) en el menú de gráficos de control para atributos.

shift.flaws <- aggregate(flaws ~ ushift,
    data = ss.data.thickness2, 
    sum, 
    na.rm = TRUE)[,2]
shift.inspected <- aggregate(flaws ~ ushift,
    data = ss.data.thickness2, 
    function(x) {
      sum(!is.na(x))
    })[,2]
thick.u <- qcc(data = shift.flaws,
    type = "u",
    sizes = shift.inspected)
plot(thick.u)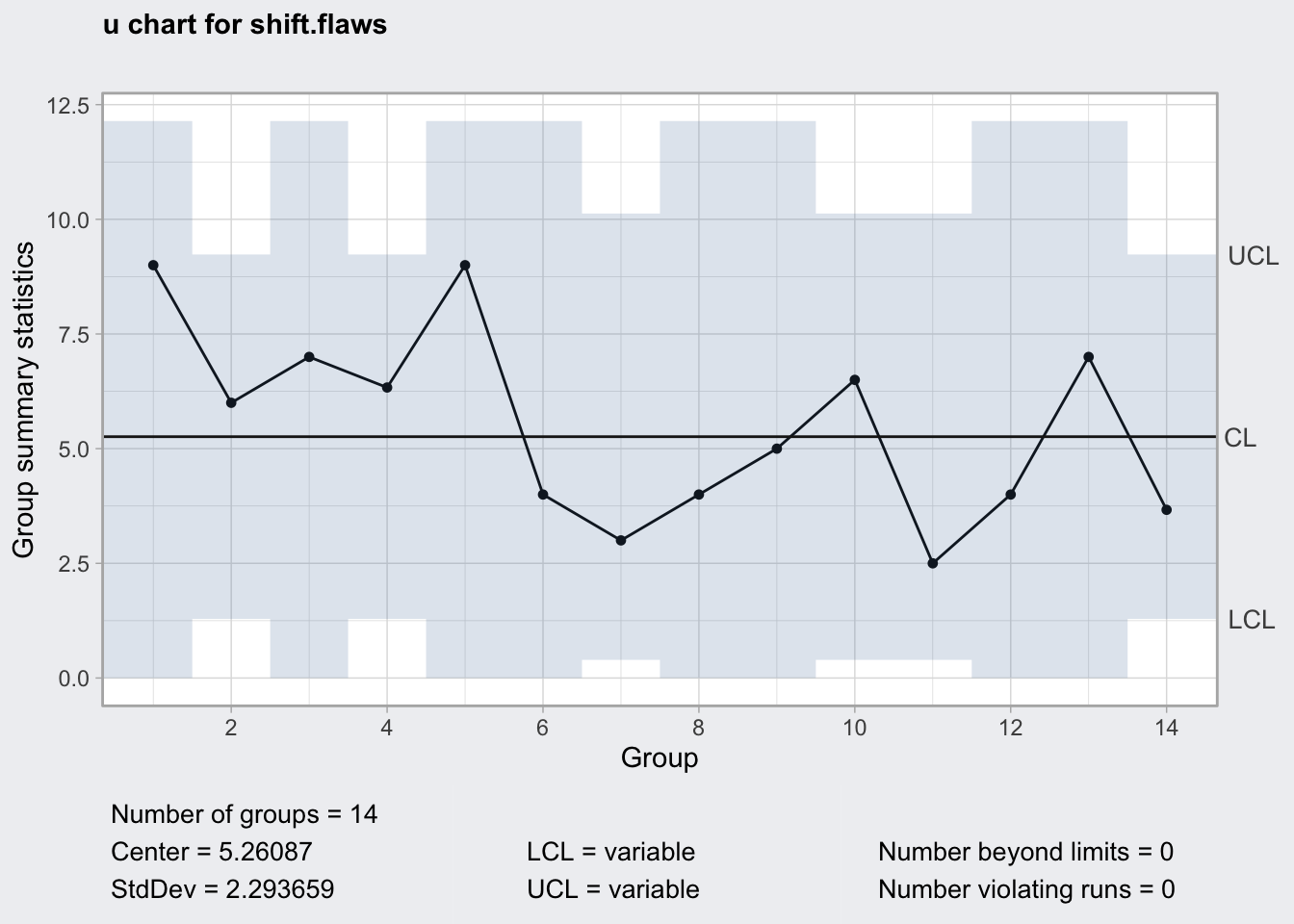

Figura 14.11: Gráfico u de los defectos por unidad

14.1.4 Estrategia SPC con gráficos de control

A medida que aumenta nuestro conocimiento del proceso y la práctica con los datos, es fácil discernir qué gráfico es el adecuado para el proceso a controlar. La figura 14.12 muestra un esquema para la selección del gráfico.

Figura 14.12: Selección del gráfico de control

La figura 14.13¹¹⁰ sintetiza el modo de proceder para una estrategia de SPC basada en gráficos de control.

Figura 14.13: Estrategia SPC

14.2 Capacidad y rendimiento de procesos

14.2.1 Control vs Especificación

14.2.1.1 La voz del cliente

En el capítulo ?? insistíamos en la necesidad de distinguir entre límites de control y límites de especificación. Los límites de especificación son la voz del cliente (VoC, Voice of the Customer). Ya sabemos que un proceso bajo control puede no cumplir con las especificaciones adecuadamente, y sin embargo un proceso que no está bajo control puede ser perfectamente capaz de cumplir con las especificaciones. En el primer caso, se deben realizar proyectos de mejora específicos para reducir la variabiliad del proceso. En el segundo, hay que detectar y eliminar las causas especiales de variación ya que si no a la larga es posible que no se cumplan las especificaciones.

La definición de los límites de especificación no suele ser una tarea fácil. En un extremo tendremos casos en los que estos límites estarán establecidos por contrato. En el otro extremo no tendremos información a priori sobre lo que el cliente espera y se tendrán que establecer los límites mediante técnicas de investigación de mercado. Además podemos tener límites de especificación determinados por la legislación o las normas aplicables. Por otra parte, podemos tener especificaciones en requisitos del producto final (las \(Y\) del proceso) o en variables críticas (las \(X\) del proceso).

La determinación de los límites de especificación de un proceso queda fuera de los contenidos de este curso, por lo que a continuación asumimos que tenemos bien definidos estos límites de especificación. Como referencia, el diseño robusto de Taguchi es uno de los métodos más ampliamente utilizados. Véase, por ejemplo, la norma ISO 16336:2014 Applications of statistical and related methods to new technology and product development process – Robust parameter design (RPD)¹¹¹, o un método más sencillo en Cano, Moguerza, and Corcoba¹¹².

En general, tendremos un objetivo para la característica crítica para la calidad (CTQ) de interés. Cuanto más se acerque nuestro proceso a ese objetivo (T, Target) o valor ideal, mejor estaremos cumpliendo las especificaciones del cliente. Por otra parte, sabemos que los procesos están sujetos a variabilidad, y por lo tanto no siempre será posible obtener un valor igual al objetivo¹¹³. Igual que nuestro proceso varía, también los requisitos tienen una cierta tolerancia. En general tenemos tres tipos de procesos en función de esta tolerancia:

• Valor ideal. En este caso tendremos límites superior (\(U\)) e inferior (\(L\)) de especificación. Por ejemplo, contenido en sal.
• Cuanto más bajo mejor. En este caso tendremos sólo límite superior de especificación. Por ejemplo, tiempo de servicio.
• Cuanto más alto mejor. Al contrario que en el caso anterior, sólo tendremos un límite de especificación inferior. Por ejemplo, la resistencia a la tensión de un envase de plástico.

En lo sucesivo nos referiremos por simplicidad a procesos con límites superior e inferior de especificación, véase la figura 14.14. El razonamiento para procesos con un sólo límite de especificación es análogo, si bien los cálculos pueden diferir según el caso.

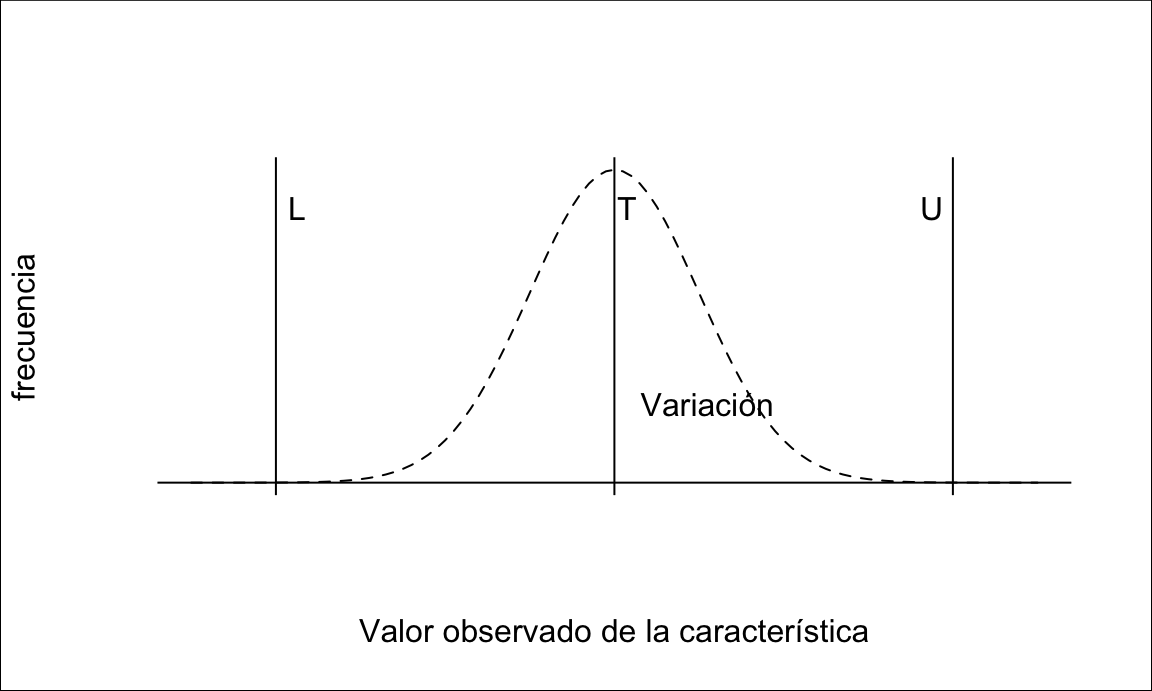
Figura 14.14: Límites de especificación de una característica (VoC)

14.2.1.2 La voz del proceso

La voz del cliente queda determinada por los límites de especificación. La voz del proceso queda determinada por el modelo que siguen los datos de nuestro proceso. Es importante señalar que lo que interesa en Control Estadístico de Procesos es el desempeño del proceso a largo plazo. Los datos concretos de un día, un lote, etc. son una muestra de nuestro proceso que nos puede estar dando un resultado satisfactorio, pero de la que tenemos que saber obtener el modelo de nuestro proceso para tomar decisiones. El modelo quedará determinado por unos pocos parámetros y una familia de distribuciones de probabilidad, por ejemplo la distribución normal con una media y desviación típica determinadas.

Por ejemplo, considérese un proceso que tiene la forma de la figura 14.15. Dado que lo que tenemos en cada conjunto de datos es una muestra de nuestro proceso, con valores concretos, podremos comprobar cada uno de estos valores y ver si está dentro de los límites de especificación. Así, podemos contabilizar el número de unidades fuera de especificación y calcular cuál ha sido el coste contable de esa muestra. Sin embargo, lo que nos interesa es saber cuál es el número esperado de no conformidades a largo plazo, dada esa distribución de probabilidad y, posiblemente, cuál es la pérdida del proceso bajo el enfoque de Taguchi, véase la figura 14.16 y la justificación en el capítulo ??.

set.seed(666)
merma1 <- round(rnorm(50, 5, 0.5), 3)
merma2 <- round(rgamma(50, shape = 25, rate = 5), 3)
merma <- data.frame(merma1, merma2)
set.seed(2017)
varlongterml <- lapply(1:10, function(i){
          data.frame(grupo = factor(i), valor=rnorm(20, rnorm(1, 90, 2), 2))
        })
varlongterm <- do.call(rbind, varlongterml)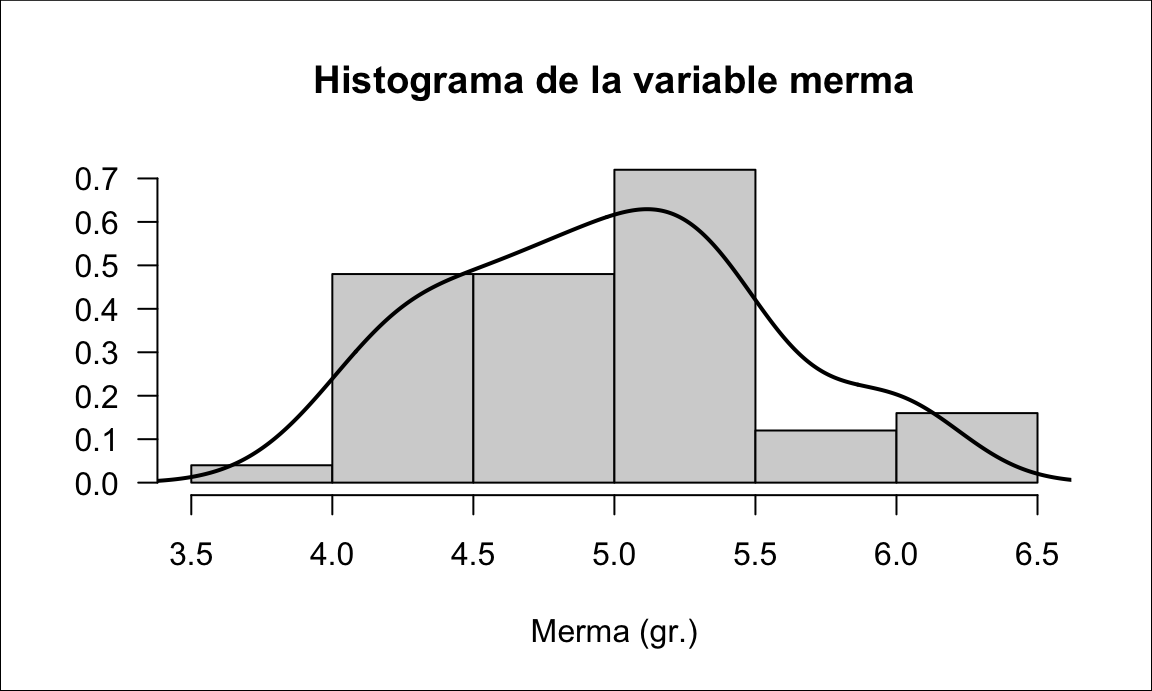

Figura 14.15: La voz del proceso (VoP)

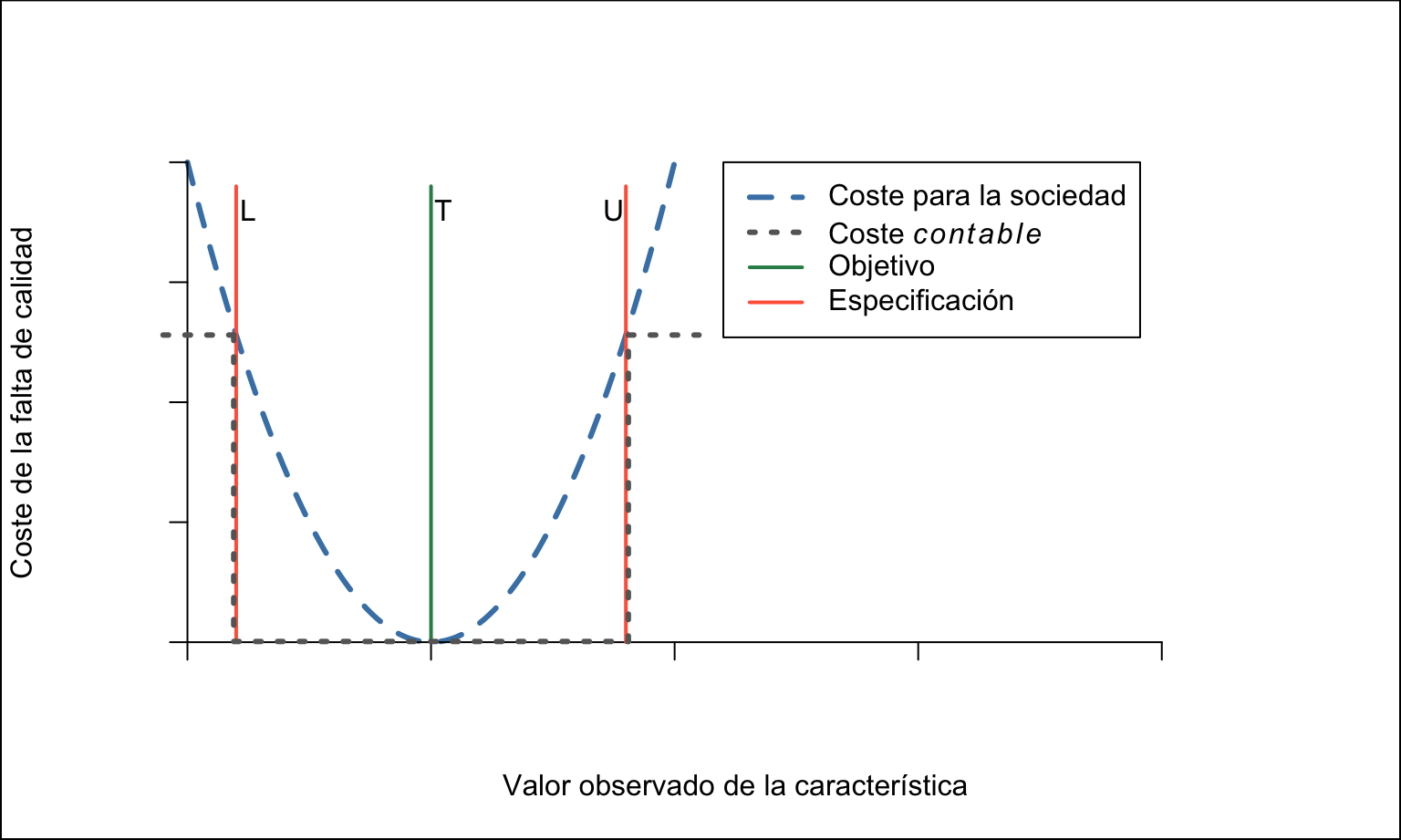
Figura 14.16: Función de pérdida de Taguchi

Veamos algunas formas de medir el rendimiento del proceso a través de los datos concretos de una muestra frente a la especificación. La forma más sencilla de medir el rendimiento de un proceso es mediante la proporción de productos conformes. Ahora bien, para reflejar el desempeño del proceso en su conjunto, y no sólo en su resultado final, debemos reflejar también como defectos aquellas unidades que hemos tenido que reprocesar o desechar en pasos intermedios del proceso (rendimiento a la primera). Por otra parte, cuando un proceso está compuesto de varios subprocesos, el rendimiento del proceso global será el producto de los rendimientos a lo largo de la cadena de \(n\) subprocesos (rendimiento encadenado)¹¹⁴.

\[Y=\frac{\text{total}-\text{defectos}}{\text{total}}\]

\[FTY=\frac{\text{total}-\text{reprocesos}-\text{defectos}}{\text{total}}\] \[RTY=\prod_{i=1}^n FTY_i = FTY_1 \times FTY_2 \times \cdots \times FTY_{n-1} \times FTY_n\]

Muchas veces en vez de medir el rendimiento de un proceso, interesa centrarse en lo contrario: la proporción de defectos, a la que podemos llamar defectos por unidad. Esta medida tiene un problema a la hora de comparar productos y servicios heterogéneos, por ejemplo por estar formados por un diferente número de componentes. Para solucionar este problema se utiliza la proporción de defectos por el número de oportunidades de que se produzca el defecto. Y más concretamente, el número de defectos por millón de oportunidades, simplemente multiplicando por 10\(^6\).

\[DPU=1-FTY=\frac{defectos}{total}\]

\[DPO=\frac{\text{número de defectos}}{\text{Número de oportunidades}}\]

\[DPMO=DPO \times 10^6\]

Estos datos los podemos calcular exactamente para una muestra concreta del proceso. Para sacar conclusiones y tomar decisiones respecto del proceso a largo plazo, necesitamos estudiar la variabilidad del proceso, y así podremos calcular estas métricas (proporción de defectos, número de defectos, etc.) esperadas a largo plazo.

14.2.1.3 Capacidad y rendimiento

Mediremos el rendimiento y la capacidad del proceso comparando la voz del cliente con la voz del proceso mediante el cálculo de ciertos índices. La capacidad del proceso deberíamos medirla solamente cuando el proceso esté bajo control estadístico, tal y como hemos visto en el capítulo ??. Así, distinguimos entre capacidad y rendimiento como:

• Condiciones de Rendimiento (performance): Índices \(P_{xx}\). Se utiliza la variabilidad a largo plazo (LT). No hace falta que el proceso esté bajo control.

• Condiciones de Capacidad (capability): Índices \(C_{xx}\). Se utiliza la variabilidad a corto plazo (ST). Es necesario que el proceso esté bajo control, y tomar subgrupos racionales.

Las fórmulas de los dos tipos de índices van a ser básicamente las mismas. La diferencia va a residir en la forma de estimar la desviación típica. Para los índices de rendimiento utilizamos la desviación típica total, sin tener en cuenta grupos.

\[\hat{\sigma}_{LT}=s=\frac{\sum (x_i - \overline{x})^2}{n-1}.\]

Para los índices de capacidad, necesitamos tener subgrupos, calcular la desviación típica dentro de cada subgrupo, \(s_i\) y después estimar la desviación típica a corto plazo con alguno de los siguientes métodos:

\[\hat{\sigma}_{ST}=\sqrt\frac{\sum s_i^2 }{m} \qquad \text{o bien} \quad \frac{\overline{R}}{d_2}, \frac{\overline{s}}{c_4}\]

En la figura ?? del capítulo ?? se mostraba un ejemplo de variación a corto y a largo plazo. La variación a largo plazo, de todos los datos, resultaba ser \(2.75\), mayor que cualquiera de la de los subgrupos. La variación a corto plazo del proceso es un resumen de la variación de todos los subgrupos, por ejemplo:

\(\sigma_{ST} = \sqrt\frac{2.1^2 + 2.32^2 + 2.08^2 + 2.51^2 + 1.71^2 + 1.66^2 + 1.78^2 + 1.57^2 + 1.67^2 + 1.09^2}{10}=1.85\)

que siempre va a ser menor que la variación a largo plazo. Cuanto más se parezcan estos dos valores, más estable es el proceso.

14.2.2 Índices de capacidad y rendimiento

Los índices de capacidad y rendimiento sin ajustar \(C_p\) y \(P_p\) se calculan dividiendo la amplitud de los límites de especificación entre la amplitud de los límites de referencia del proceso. Por simplicidad en la exposición, vamos a considerar que la característica en estudio sigue una distribución normal, y entonces esta amplitud es precisamente seis veces la desviación típica del proceso, véase la figura 14.17. Para distribuciones no normales, esta amplitud se calculará como \(X_{99.865\%} - X_{0.135\%}\), es decir, la direrencia entre el percentil \(99.865\) y el percentil \(0.135\). Entonces:

\[C_p = \frac{U-L}{6\sigma_{ST}},\] \[P_p = \frac{U-L}{6\sigma_{LT}}.\]

Es decir, el índice nos dice cuántas veces caben seis desviaciones típicas dentro de las especificaciones. En un proceso cuya distribución (modelo) es normal, un índice igual a 1 implica que la proporción de defectos es del 0.27%.

Los índices sin ajustar no permite comprobar si el proceso está centrado en el objetivo, lo cual es deseable en procesos con límites simétricos. Para solucionarlo se utilizan los índices ajustados \(C_{pk}\) y \(P_{pk}\) cuya interpretación es similar, pero donde tenemos en cuenta sólo el lado hacia el que el proceso es menos capaz. Es decir, calculamos primero los índices superior e inferior:

\[C_{pU} = \frac{U-\mu}{3\sigma_{ST}},\quad C_{pL} = \frac{\mu - L}{3\sigma_{ST}},\] \[P_{pU} = \frac{U-\mu}{3\sigma_{LT}},\quad P_{pL} = \frac{\mu - L}{3\sigma_{LT}},\] y entonces el índice de capacidad ajustado es el mínimo de los dos:

\[C_{pk} = \min\{C_{pU}, C_{pL}\},\] \[P_{pk} = \min\{P_{pU}, P_{pL}\}.\]

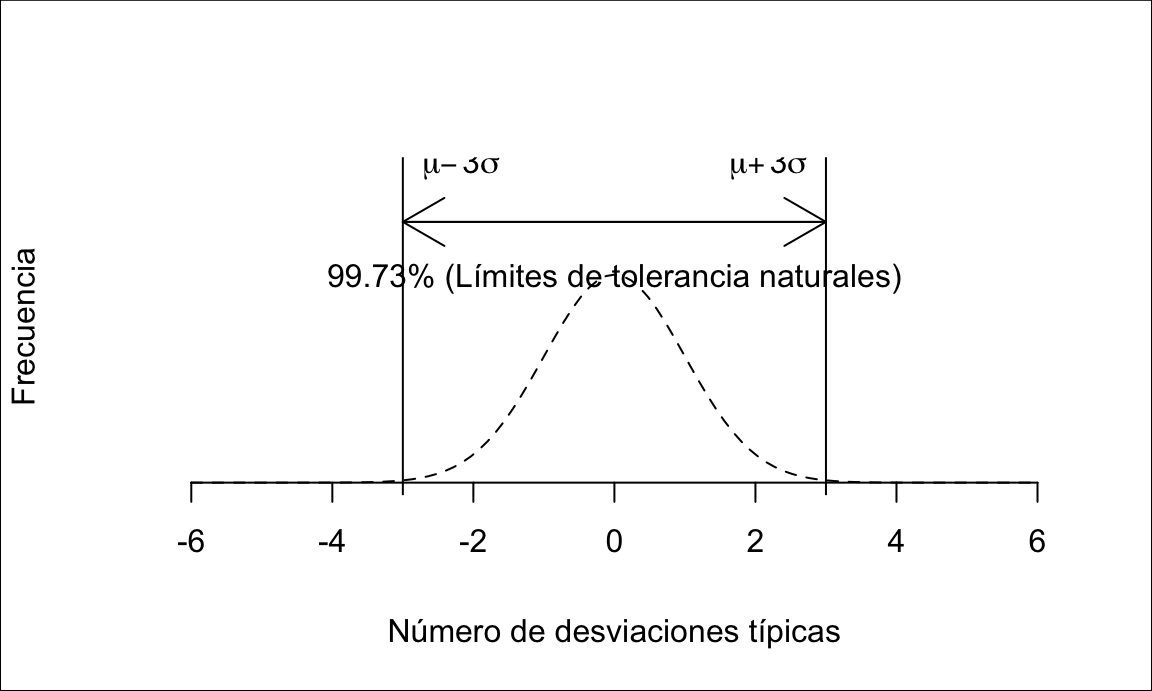
Figura 14.17: Límites de referencia del proceso

Para el cálculo de los índices podemos utilizar valores pre-especificados de la media (\(\mu_0\)) y la desviación típica (\(\sigma_0\)), o estimarlos mediante la media muestral \(\overline{X}\) y la desviación típica a corto y a largo plazo como se ha indicado arriba.

Los índices anteriores asumen que el objetivo es el centro de los límites de especificación. En algunas situaciones, el objetivo es otro valor distinto (véase la figura 14.18) y entonces utilizamos el índice \(C_{pm}\), también conocido como índice de capacidad de Taguchi, y que se puede obtener a partir de los índices anteriores, por ejemplo para los índices de capacidad:

\[C_{pm}=\frac{C_p}{\sqrt{1+\left (\frac{\mu-T}{\sigma} \right )^2}},\]

\[C_{pkm}=\frac{C_{pk}}{\sqrt{1+\left (\frac{\mu-T}{\sigma} \right )^2}}.\]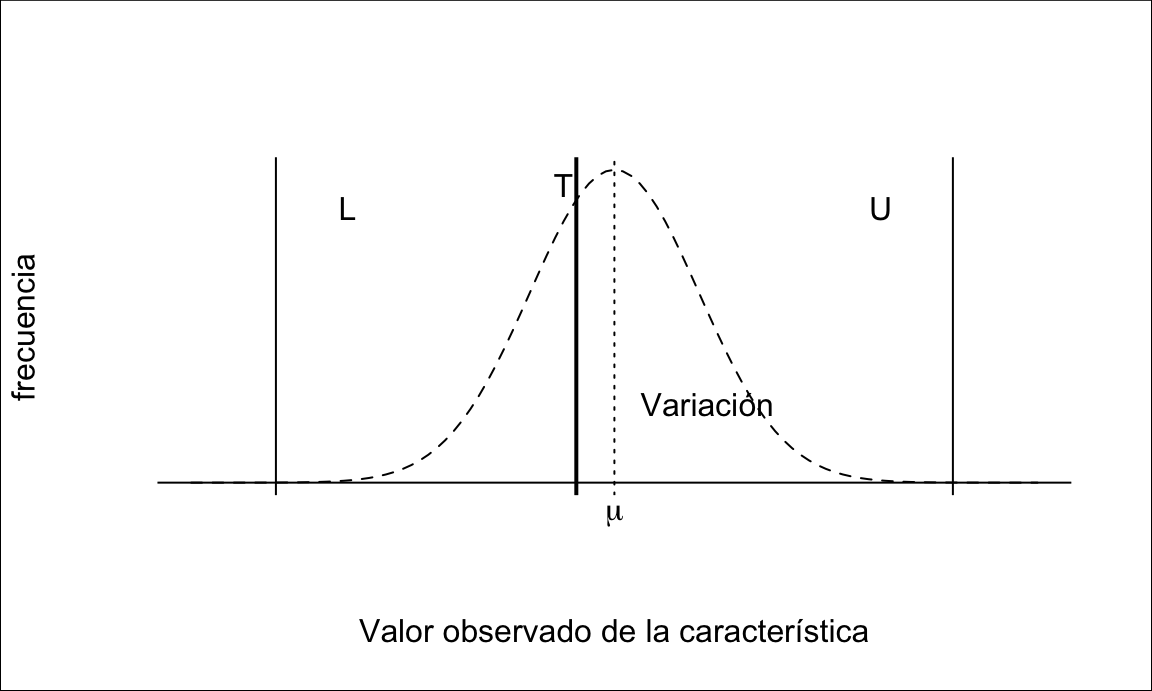

Figura 14.18: Objetivo de la característica no centrado en el punto central de la especificación

14.2.2.1 Interpretación de los índices

Normalmente se calculan todos los índices que sean apropiados para el proceso, y se analizan conjuntamente:

1. Los índices de rendimiento, que se pueden calcular siempre.
2. Los índices de capacidad, solo cuando el proceso está bajo control estadístico.
3. Los índices de Taguchi, cuando el objetivo no está en el centro de la especificación.

A partir de los índices, se pueden realizar las siguientes comparaciones importantes:

• Comparar índices de rendimiento e índices de capacidad. Los primeros indican el rendimiento real del proceso, mientras que los segundos indican el rendimiento potencial que podríamos alcanzar si la variabilidad a largo plazo fuese igual a la variabilidad a corto plazo.
• Compara índices corregidos con índices sin corregir. Cuanto más se parezcan, más centrado estará nuestro proceso en la especificación, lo que siempre es deseable.

Además, la interpretación numérica del índice nos indicará cuánto es de capaz nuestro proceso, según los valores que tome:

• El índice es aproximadamente igual a 1. La variación natural del proceso producirá una proporción de no conformidades equivalente a la probabilidad de estar fuera de los límites de control
• El índice es mayor que 1. El proceso es capaz de cumplir las especificaciones más allá de los límites naturales de variación
• El índice es menor que 1. El proceso no es capaz de cumplir las especificaciones y se producirán muchas no conformidades por la simple variación natural del proceso

El valor ideal para los índices de control depende de la naturaleza del proceso. Un valor de referencia generalmente aceptado como bueno es 1.33, siendo 1.64 un valor muy bueno. Lo vemos gráficamente en la figura 14.19.

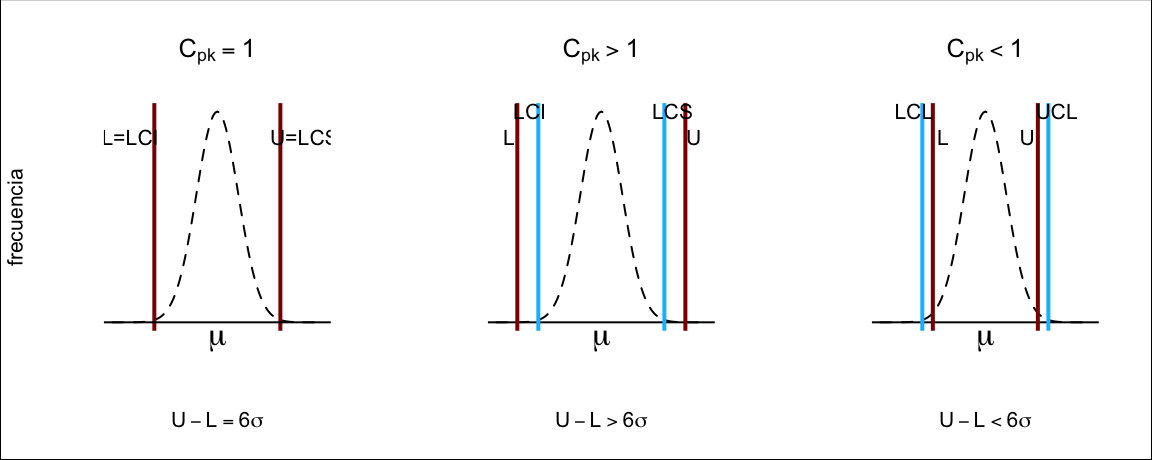
Figura 14.19: Interpretación de los índices de capacidad

Es importante tener en cuenta que los valores obtenidos de los índices de capacidd son estimaciones obtenidas a partir de muestras. Por tanto, están sujetos a error, y antes de tomar decisiones es aconsejable mirar los intervalos de confianza para estas estimaciones. Por ejemplo, podemos tener un índice \(C_{pk} = 1.1\) y tomar la decisión de dejar la inspección 100%. Pero si el intervalo de confianza fuera, por ejemplo, \([0.9, 1.2]\), significaría que el índice podría ser menor que 1 para cierto nivel de confianza en futuras muestras, por lo que incurrimos en riesgos altos si asumimos que el proceso es capaz.

14.2.2.2 La sigma del proceso

Una medida muy utilizada en mejora de procesos es la sigma del proceso, o Z-score, que se calcula de forma similar al índice de capacidad:

\[Z=\min \left \{ \frac{(USL-\mu)}{\sigma},\quad \frac{(\mu-LSL)}{\sigma} \right \}.\]

En este caso, el valor obtenido es el número de desviaciones típicas que caben entre los límites de especificación. Así, una sigma igual a 3 tiene la misma interpretación que el el índice \(C_{pk}\) igual a 1. Habitualmente se asume¹¹⁵ que hay que restar 1.5 unidades a la sigma calculada con la variabilidad a corto plazo para reflejar la variabilidad del proceso a largo plazo (\(Z_{LT}=Z_{ST} - 1.5\). Un proceso cuya sigma es igual a 6 estará produciendo sólo 3.4 DPMO (defectos por millón de oportunidades).

14.2.2.3 Estudio de capacidad

En un estudio de capacidad se debe incluir un análisis sobre la distribución de los datos, ya que se debería verificar la normalidad de los datos. La representación de los límites de especificación en el histograma suele ser muy útil visualmente. Los estudios de capacidad habitualmente utilizan los mismos datos que se han utilizado para crear los gráficos de control e identificar si el proceso está en condiciones de rendimiento o de capacidad. Se obtienen los índices para su interpretación y se calculan las métricas de rendimiento tanto reales como esperadas según la variabilidad de los datos.

R

Vamos a realizar el estudio de capacidad de los datos utilizados en los ejemplos del capítulo ?? y que se encuentran en la tabla 14.1. En el código a continuación se realiza primero un análisis exploratorio representando todas las mediciones, apreciándose la variabilidad a corto y a largo plazo (figura 14.20).

A continuación, se guardan los datos en un objeto qcc para poder utilizarlos en la función process.capability del paquete qcc, donde introducimos además los límites de especificación. La función devuelve los índices de capacidad, incluido intervalo de confianza, y otras medidas. También se muestran en la salida gráfica como muestra la figura 14.21. Este ejemplo concreto muestra un proceso con muchos errores (reales 27%, esperados 20.4%), y unos índices muy por debajo del 1, que requiere inspección 100%.

library(lattice)
dotplot(thickness ~ shift | day, 
    data = ss.data.thickness2,
    layout = c(7, 1))   

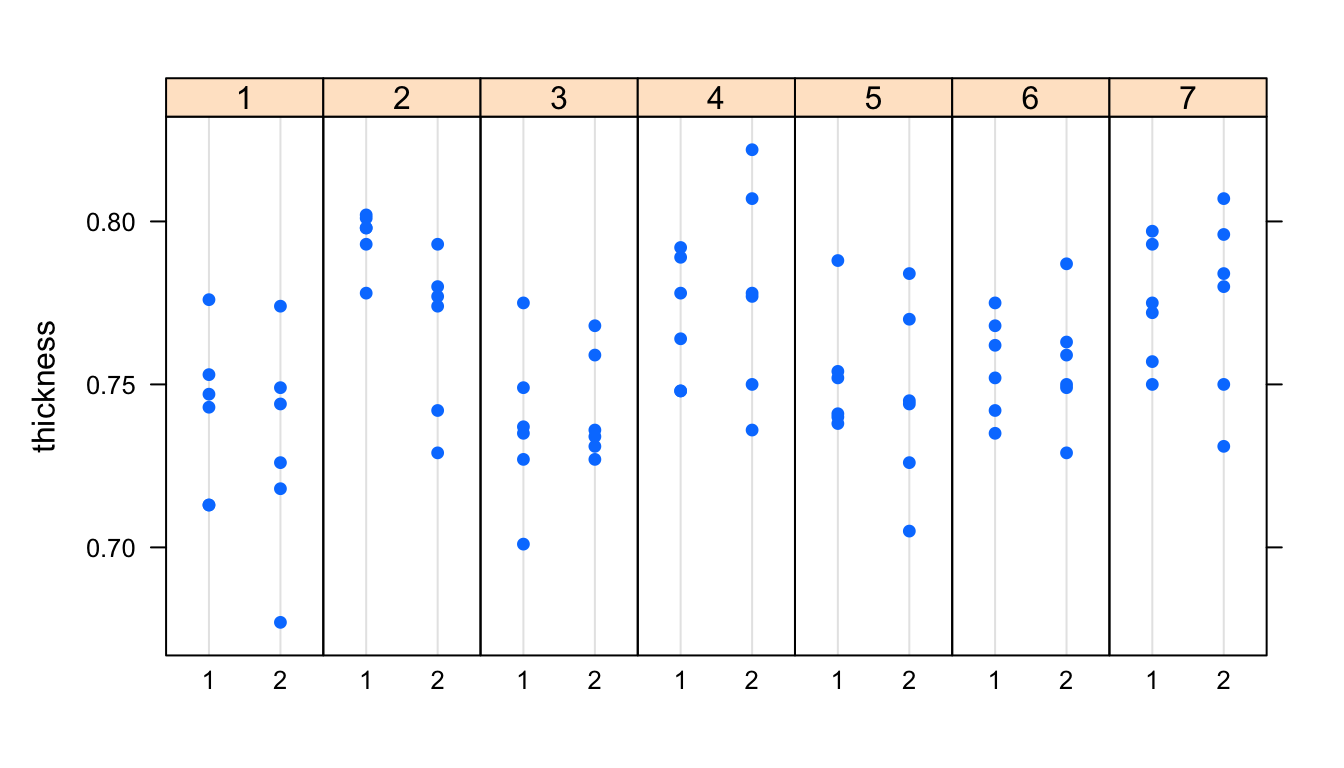
Figura 14.20: Variabilidad a corto y a largo plazo

library(qcc)
groups <- qccGroups(data = ss.data.thickness2, 
                    x = thickness, 
                    sample = ushift)
myqcc <- qcc(data = groups, type = "xbar", plot = FALSE)

cap <- processCapability(object = myqcc, 
    spec.limits = c(0.718, 0.782))
print(cap)
#> ── Process Capability Analysis ─────────────────── 
#> 
#> Number of obs = 84           Target = 0.75    
#> Center        = 0.7585238    LSL    = 0.718   
#> StdDev        = 0.02376254   USL    = 0.782   
#>                   
#> Capability indices  Value   2.5%  97.5%
#>               Cp    0.449  0.381  0.517
#>               Cp_l  0.568  0.474  0.663
#>               Cp_u  0.329  0.256  0.402
#>               Cp_k  0.329  0.242  0.416
#>               Cpm   0.423  0.355  0.490
#> 
#> Exp<LSL 0.044%    Obs<LSL 0.06%
#> Exp>USL 0.16%     Obs>USL 0.21%
plot(cap)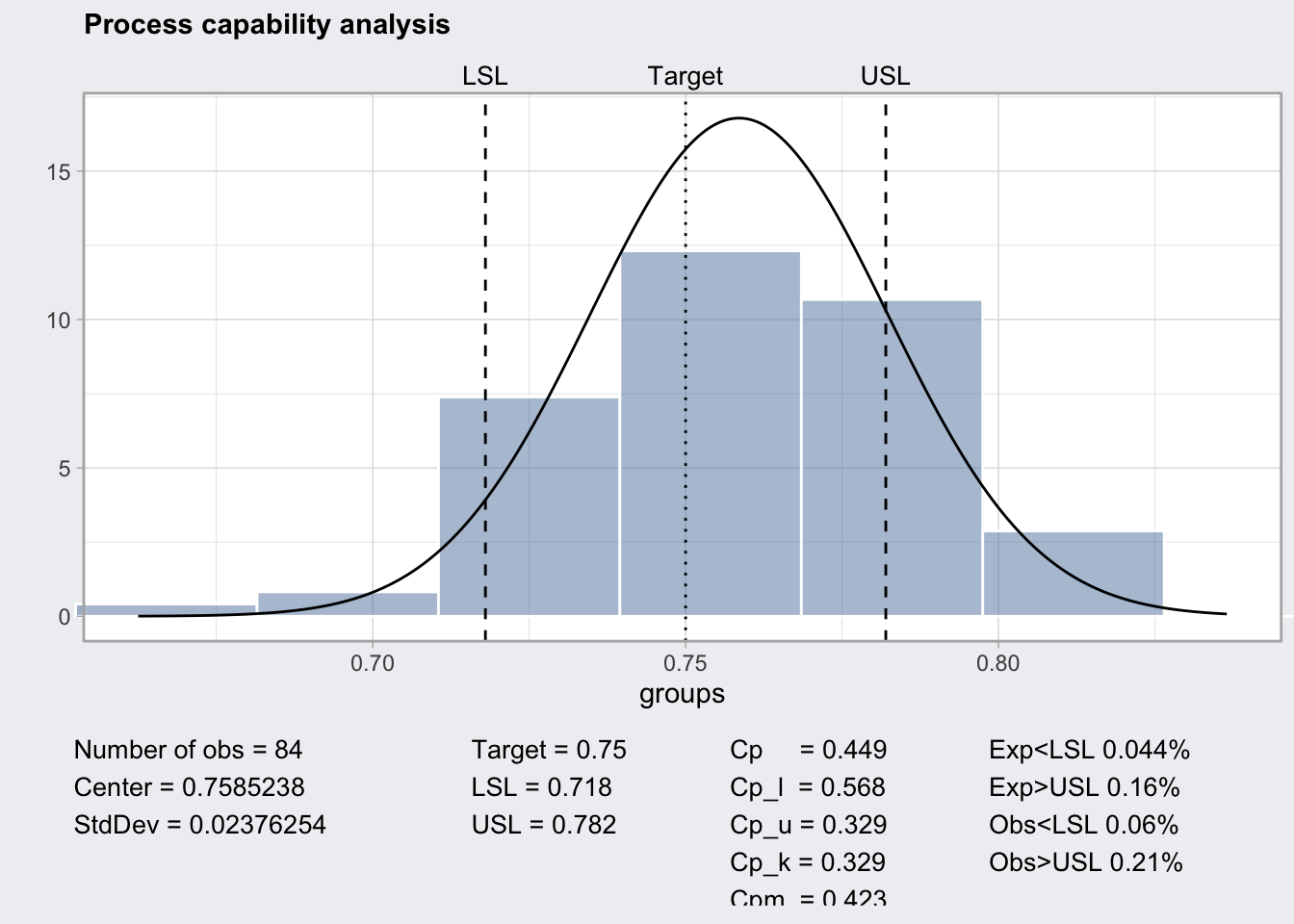
#> Warning: The dot-dot notation (`..density..`) was deprecated in
#> ggplot2 3.4.0.
#> ℹ Please use `after_stat(density)` instead.
#> ℹ The deprecated feature was likely used in the qcc
#>   package.
#>   Please report the issue at
#>   <

Figura 14.21: Estudio de capacidad para los datos del espesor

Excel

Para hacer un estudio de capacidad en Excel podemos realizar todos los cálculos aplicando las fórmulas proporcionadas. Nunca se insistirá lo suficiente en la necesidad de revisar las fórmulas en Excel para asegurarse de que están referenciando bien las celdas.

En el siguiente archivo se puede encontrar un ejemplo del estudio de capacidad de los datos del espesor de placas de acero con Excel:

http://emilio.lcano.com/b/epac/datos/ejemplos_espesor2.xlsx

Minitab

En Minitab hay varias opciones en el menú Herramientas de Calidad para realizar análisis de capacidad. El más directo es seleccionar Estadísticas > Herramientas de calidad > Análisis de capacidad > Normal. Ahí introducir la columna que contiene los datos, los tamaños de subgrupos y las especificaciones. Más opciones están disponibles, véase la ayuda.

Véase otro ejemplo reproducible aquí:

https://support.minitab.com/es-mx/minitab/18/help-and-how-to/quality-and-process-improvement/capability-analysis/how-to/capability-analysis/normal-capability-analysis/before-you-start/example/

R

Un estudio alternativo de capacidad es el que proporciona la función ss.study.ca del paquete SixSigma, más enfocado a esta medodología, en el que se pueden introducir dos conjuntos de datos (a corto y a largo) para calcular la sigma del proceso y otras métricas al estilo Seis Sigma. El siguiente código realiza un análisis de capacidad de los datos de embotellado de una bodega.

library(SixSigma)
ss.study.ca(ss.data.ca$Volume, rnorm(40, 753, 3), 
        LSL = 740, USL = 760, T = 750, alpha = 0.05, 
             f.sub = "Winery Project")

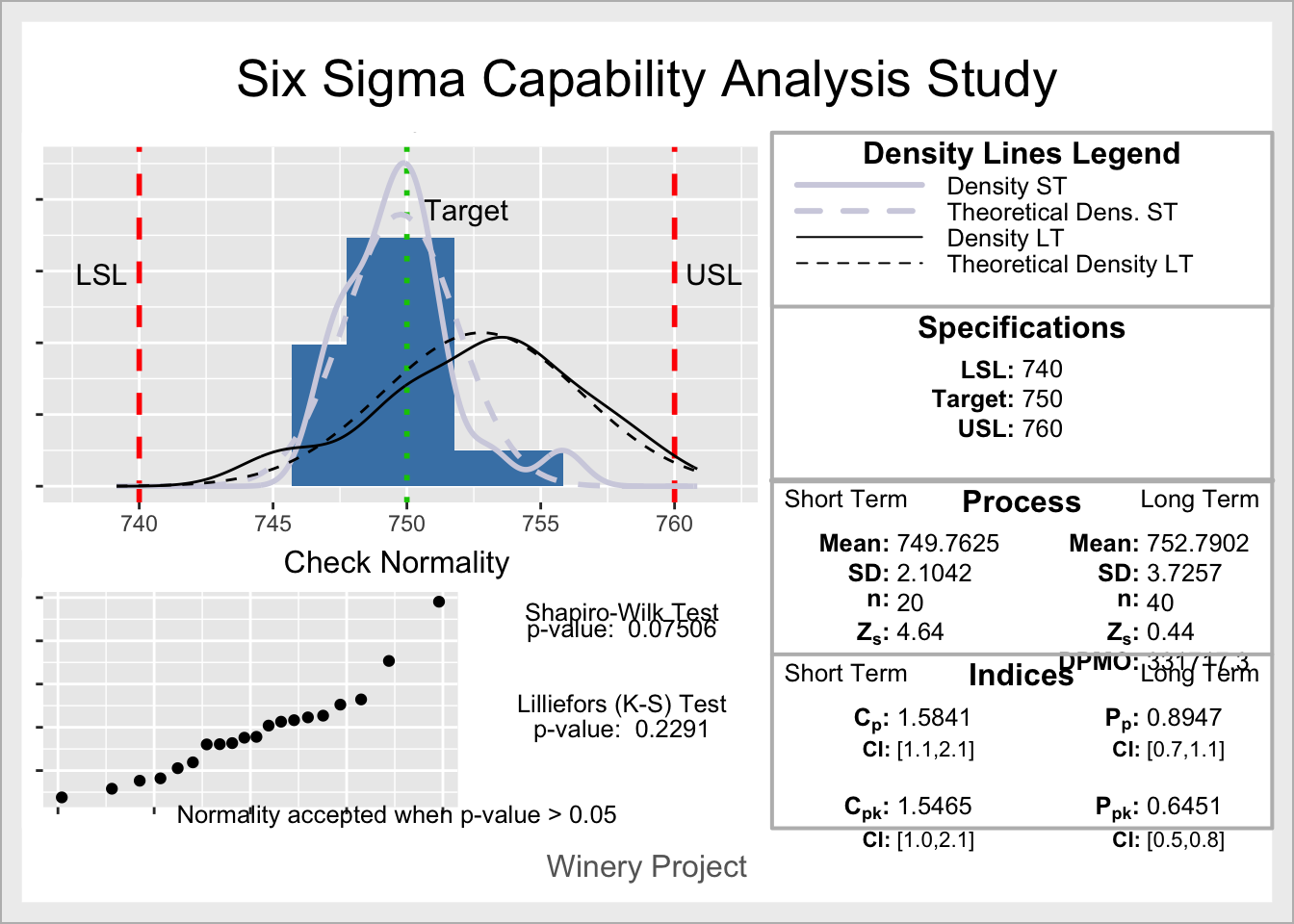
Figura 14.22: Estudio de capacidad para los datos de una bodega

Finalmente, véase la relación del análisis de capacidad con los gráficos de control y la inspección por muestreo, reflejadas en la figura 14.13 del capítulos ??.