Capítulo 7 Modelos de distribución de probabilidad

7.1 Introducción

En el capítulo 5 vimos que una variable aleatoria unidimensional se puede modelizar por cualquier función de distribución de probabilidad que cumpla los requisitos básicos de la probabilidad así, tenemos infinitas funciones de probabilidad para variables aleatorias discretas, o de densidad para variables aleatorias continuas. Sin embargo, la mayoría de los fenómenos de interés estudiados mediante la probabilidad se ajustan a un reducido conjunto de modelos de distribución de probabilidad o familias de distribuciones para los que se han determinado sus características principales, facilitando así el trabajo con variables aleatorias. En este capítulo revisaremos los más importantes para variables aleatorias discretas.

El primer paso para identificar el modelo de distribución de probabilidad más adecuado, es describir claramente la variable aleatoria \(X\), y de ahí deducir cuál es el modelo adecuado. Para cada modelo, se conoce su función de probabilidad o de densidad que contiene un número muy reducido de parámetros. A partir de esta función de probabilidad o de densidad, se deducen sus características, por ejemplo la media y la varianza, que quedan expresadas en función de dichos parámetros. Una vez identificado el modelo de distribución de probabilidad, hay que establecer los parámetros concretos que caracterizan la variable aleatoria concreta de interés. En este libro se asumen como conocidos (o deducibles fácilmente de la descripción del problema), aunque en aplicaciones reales se deberán estimar a partir de muestras representativas de la población con técnicas de inferencia estadística, que no se tratan en este texto. Una vez determinados los parámetros, podemos calcular fácilmente las características de la variable aleatoria con las fórmulas dadas, así como realizar cálculo de probabilidades utilizando todo lo aprendido hasta ahora.

Para indicar que una variable aleatoria \(X\) sigue una determinada distribución de probabilidad, utilizamos la siguiente notación:

\[X \sim \mathcal{D}\mathit{istr}(\boldsymbol{\theta}),\]

donde \(\mathcal{D}\mathit{istr}\) identifica el modelo de distribución de probabilidad, y \(\boldsymbol{\theta}\) es el vector de parámetros con los que queda totalmente definida la distribución de probabilidad de la variable aleatoria \(X\) según ese modelo de distribución. Tanto para los modelos de distribución de probababilidad discretos de este capítulo, como en los continuos del siguiente, se proporciona la función de probabilidad o de densidad de los mismos, así como la esperanza y la varianza que se deduce de las mismas (aunque no se incluye dicha deducción). El resto de características de cada modelo se puede obtener igualmente a partir de su distribución de probabilidad. Tampoco se incluyen las demostraciones de que, obviamente, las funciones de densidad y de probabilidad de cada distribución cumplen las propiedades para ser una Ley de probabilidad.

7.2 Modelos de distribución de probabilidad discretos

7.2.1 Distribución de Bernoulli

Las distribuciones de probabilidad discretas se basan de una forma u otra en procesos de Bernoulli. Un proceso de Bernoulli consiste en realizar un experimento que tiene dos resultados posibles. A uno le llamamos éxito y al otro le llamamos fracaso, y conocemos la probabilidad del suceso éxito, a la que llamamos \(p\).

Dado un proceso de Bernoulli aislado, podemos definir la variable aleatoria \(X\) que toma el valor 1 si el experimento es un éxito, y 0 si el experimento es un fracaso.

\[X= \begin{cases} 1 & \text{ si éxito con probabilidad } p\\ 0 & \text{ si fracaso} \end{cases}\] Entonces las probabilidades para los dos posibles valores de la variable serán:

\[P[X=1]=p;\quad P[X=0]=1-p,\]

y diremos que \(X\) sigue una distribución de Bernoulli de parámetro \(p\):

\[X \sim \mathit{Ber}(p);\; 0<p<1.\]

Algunas veces se utiliza la notación \(q=1-p\). Una expresión general para la función de probabilidad es la siguiente:

\[P[X = x] = p^x (1-p)^{(1-x)};\; x =0, 1.\]

Las características de posición y dispersión de esta variable aleatoria se deducen fácilmente:

• Media: \(\mu=E[X] = p\).

• Varianza: \(\sigma^2=\mathit{V}[X] = p \cdot (1-p)\).

La distribución de Bernoulli aparece en los procesos de clasificación de observaciones (individuos, empresas, etc.) en una de dos categorías.

En el ejemplo de los potenciales usuarios de nuestro servicio, dedujimos en el capítulo 4 que la probabilidad de que un cliente tomado al azar contrate el servicio era \(0.25\). Entonces la variable aleatoria:

\[X: \begin{cases}0\quad \text{ el cliente no contrata}\\1\quad \text{ el cliente contrata}\end{cases}\]

sigue una distribución de probabilidad de Bernoulli de parámetro \(p=0.25\), su media es \(\mu=0.25\), su varianza \(\sigma^2=0.1875\) y su función de probabilidad:

\[P[X=x]=0.25^x\times 0.75^{1-x}\]

El interés de la distribución de Bernoulli también está en las distribuciones de probabilidad derivadas de ella cuando repetimos el proceso bajo distintas condiciones. En los siguientes apartados veremos algunas de estas distribuciones que se extienden a partir de la de Bernoulli.

7.2.2 Distribución binomial

Partiendo de un proceso de Bernoulli, consideremos la repetición del experimento \(n\) veces, y que el resultado de cada experimento es independiente de los demás. Entonces, la variable aleatoria \(X\): Número de éxitos en \(n\) pruebas independientes de Bernoulli con probabilidad de éxito \(p\) cada una de ellas sigue una distribución de probabilidad binomial de parámetros \(n\) y \(p\):

\[X \sim \mathit{Bin}(n;\;p);\; n> 0,\;0<p<1. \]

Nótese que la distribución de Bernoulli es un caso particular de la binomial cuando \(n=1\).

\[\mathit{Ber}(p) = \mathit{Bin}(1;\;p).\]

A su vez, la distribución binomial es la suma de \(n\) variables aleatorias independientes de Bernoulli:

\[ \implies \mathit{Bin}(n;\;p) = \sum\limits_{i=1}^n X_i :\; X_i \sim \mathit{Ber}(p)\; \forall\, i,\]

de donde llegamos a la siguiente expresión de la función de probabilidad:

\[\boxed{P[X = x] = \binom{n}{x}\cdot p^x \cdot (1-p)^{(n-x)};\; x = 0, 1, \ldots, n},\]

donde:

\[\binom{n}{x}=\frac{n!}{x!(n-x)!},\]

conocido como número combinatorio o coeficiente binomial. En el apéndice D.2 se encuentran algunas propiedades de este coeficiente, que se puede calcular fácilmente en las calculadoras científicas con la tecla nCr.

Nótese que en la fórmula de la función de probabilidad de la distribución binomial aparecen muchos conceptos de probabilidad aprendidos hasta ahora. Como son sucesos independientes, \(p^x\) es la probabilidad de la intersección de \(x\) éxitos, y \((1-p)^{n-x}\), la probabilidad de la intersección de \({n-x}\) fracasos. Entonces \(p^x \cdot (1-p)^{(n-x)}\) es la probabilidad de una de las ordenaciones posibles. Como el orden de éxitos y fracasos nos da igual, la probabilidad que nos interesa es la probabilidad de la unión de todas las ordenaciones posibles que, como son sucesos disjuntos, se corresponde con la suma de probabilidades. Estas probabilidades son todas iguales, y el número de ordenaciones posibles es \(\binom{n}{x}\), por eso multiplicamos.

La figura 7.1 muestra gráficamente la distribución de probabilidad para varios valores de \(n\) y \(p\).

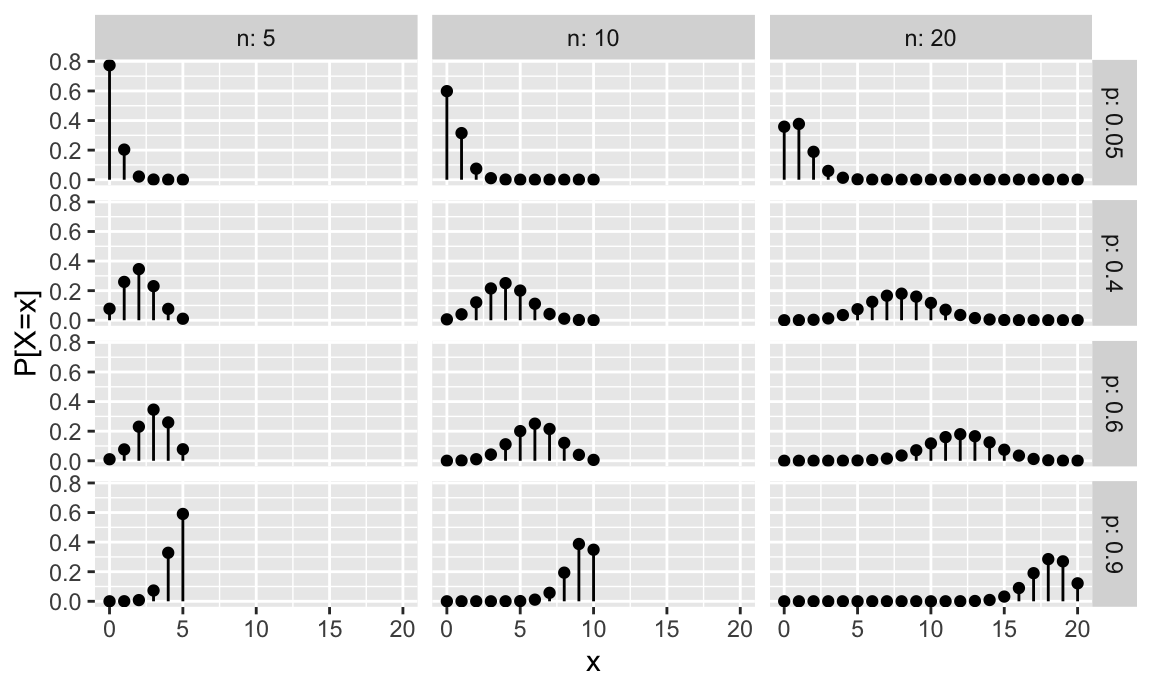
Figura 7.1: Representación de la función de probabilidad del modelo binomial

Las caracterísiticas principales de la distribución binomial se deducen fácilmente aplicando las fórmulas de la esperanza matemática vistas en el capítulo 5, y son:

• Media: \(\mu=E[X] = n\cdot p.\)

• Varianza: \(\sigma^2=\mathit{V}[X] = n\cdot p\cdot (1-p).\)

La distribución binomial, además, cumple la propiedad aditiva, es decir, la suma de \(m\) variables aleatorias binomiales con idéntico parámetro \(p\) y, posiblemente, distintos parámetros \(n_j, \, j=1, \ldots, m\), es una distribución binomial de modo que:

\[Y=\sum\limits_{j=1}^m {X_j},\, X_j \sim \mathit{Bin}(n_j;\;p) \implies Y \sim \mathit{Bin}\left ( \sum\limits_{j=1}^m n_j;\; p \right ).\] Esta propiedad, que iremos viendo en casi todos los modelos, es muy importante porque nos permite resolver problemas de probabilidad en los que que se repiten las realizaciones de las variables aleatorias, lo que nos interesa es el total. No hay que confundir la suma de variables aleatorias con la mezcla de poblaciones en los que hay que aplicar los teoremas de la probabilidad total y de Bayes.

Supongamos que la probabilidad de que un estudiante acabe un grado en Ciencias es de \(0.4\). Tomamos al azar un grupo de 5 estudiantes. ¿Cuál es la probabilidad de que ninguno obtenga el grado? ¿Y la probabilidad de que al menos dos lo obtengan?

Si definimos la variable aleatoria \(X:\) Número de estudiantes que obtienen el grado de un grupo de 5, entonces \(X\) sigue la distribución:

\[X\sim \mathit{Bin}(5;\; 0.4);\; x = 0, 1, 2, 3, 4, 5\]

y por tanto las probabilidades pedidas son, respectivamente:

\[P[X=0]=\binom{n}{x}\cdot p^x \cdot (1-p)^{(n-x)}=\binom{5}{0}\cdot 0.4^0 \cdot (0.6)^5\simeq0.0776.\]

\[P[X\geq 2]=1-P[X < 2] = 1-\left [ P[X=0] + P[X=1]\right]=\] \[=1-\left[ 0.0778 + \binom{5}{1}\cdot 0.4^1 \cdot 0.6^4\right] \simeq 0.6630.\]

HOJA DE CÁLCULO

En las aplicaciones de hoja de cálculo, tenemos funciones que devuelven la densidad (probabilidad en modelos discretos) y la probabilidad acumulada (función de distribución) de los modelos de distribución de probabilidad más utilizados. Puede diferir el nombre de la función entre diferentes programas. En Hojas de Cálculo de Google y LibreOffice se obtendrían las probabilidades del ejemplo así:

=BINOM.DIST(0;5;0,4;0)

=1-BINOM.DIST(1;5;0,4;1)

Mientras que en EXCEL la función se llama DISTR.BINOM.N:

=DISTR.BINOM.N(0;5;0,4;)

=1-DISTR.BINOM.N(1;5;0,4;VERDADERO)

R

En R, para cada modelo de distribución de probabilidad tenemos una función que empieza por d y devuelve la “densidad” (probabilidad en el caso de discretas) y otra que empieza por p y devuelve la “probabilidad (acumulada)”, es decir, la función de distribución (o su complementario). Después de la d o la p vendrá el nombre (o abreviatura) del modelo de probabilidad, por ejemplo para la binomial binom. Entonces la función dbinom devuelve la probabilidad para un valor de la variable aleatoria. A las funciones hay que pasarle también los parámetros del modelo de distribución. En el caso de la binomial, el parámetro p y el parámetro n. A continuación se muestran las expresiones que calculan las probabliidades del ejemplo. Véase cómo la segunda probabilidad se puede calcular de varias formas, utilizando el complementario como en la hoja de cálculo, el argumento lower.tail de la función dbinom, o sumando las probabilidades para los valores que cumplen la condición.

Para cada modelo de distribución de probabilidad tenemos otras dos funciones, una que empieza por q, que calcula el cuantil dada una probabilidad acumulada (es decir, es la función inversa de la función de distribución) y otra que empieza por r, con la que podemos obtener valores aleatorios (random) o simulaciones de una variable aleatoria.

dbinom(x = 0, size = 5, prob = 0.4)
#> [1] 0.07776
1 - pbinom(q = 1, size = 5, prob = 0.4)
#> [1] 0.66304
pbinom(q = 1, size = 5, prob = 0.4, lower.tail = FALSE)
#> [1] 0.66304
sum(dbinom(x = 2:5, size = 5, prob = 0.4))
#> [1] 0.66304

Selecciono 10 potenciales sujetos del estudio al azar. ¿Cuál es la probabilidad de que al menos uno responda al tratamiento?

En términos de variable aleatoria:

• \(X\): Número de éxitos en 10 experimentos independientes de Bernoulli con probabilidad de éxito 0.25
• \(X \sim \mathit{Bin(10;\; 0.25)}\)
• \(P[X \geq 1] = 1- P[X < 1] = 1-P[X=0] \simeq 1- 0.0563 \simeq 0.9437\)

HOJA DE CÁLCULO

[LibreOffice] =1-BINOM.DIST(0;10;0,25;1)

[EXCEL] =1-DISTR.BINOM.N(0;10;0,25;VERDADERO)

R

La siguiente expresión calcula la probabilidad buscada. El lector puede probar otros caminos para llegar a la misma probabilidad, como en el ejemplo anterior.

pbinom(q = 0, size = 10, prob = 0.25, lower.tail = FALSE)
#> [1] 0.9436865

Hay tres consideraciones muy importantes a la hora de resolver ejercicios en variables discretas:

1. Es muy importante tener claro cuáles son los posibles valores de la variable aleatoria, y así saber qué probabilidades hay que calcular.

2. Es posible llegar al resultado de varias formas posibles, y hay que pararse a pensar cuál será la más rápida, usando las propiedades de la probabilidad (principalmente: probabilidad del suceso complementario y probabilidad de la unión de sucesos disjuntos).

3. Al cambiar de una probabilidad a la del suceso contrario, es muy importante tener en cuenta si las desigualdades incluyen el símbolo igual.

7.2.3 Distribución de Poisson

La distribución de Poisson surge inicialmente como distribución límite de la binomial cuando \(n\) tiende a infinito y \(p\) se mantiene estable. Posteriormente se vio que describe muy bien los procesos donde se cuentan el número de ocurrencias de un evento por unidad (de tiempo, espacio, …). La probabilidad de ocurrencia en un instante concreto es muy baja, pero en un intervalo determinado es muy probable que suceda varias veces. Bajo estas circunstancias, la variable aleatoria:

\[X: \text{ Número de eventos por unidad}\] sigue una distribución de Poisson:

\[X \sim \mathit{Poiss}(\lambda);\; \lambda >0, \]

donde el único parámetros \(\lambda\) es la media y la varianza de la variable aleatoria. Es decir, se producen, de media, \(\lambda\) eventos por unidad de tiempo, superficie, etc. La distribución de Poisson tiene la siguiente función de probabilidad:

\[\boxed{P[X = x] = \frac{e^{-\lambda}\lambda^x}{x!};\; x = 0, 1, \ldots\ \infty}.\]

El estadístico ruso L. Bortkewicz explicó en 1898 que la distribución de Poisson describía muy bien el número de muertes producidas por coces de caballo en las guerras prusianas.

La figura 7.1 muestra gráficamente la distribución de probabilidad para varios valores de \(n\) y \(p\). Se representan valores desde \(x=0\) hasta \(x= \mu + 4\sigma\). Aunque teóricamente los posibles valores son hasta infinito, a partir de ese valor la probabilidad es prácticamente cero. Para valores de \(\lambda\) grandes, esto también sucede en los valores de \(x\) bajos.

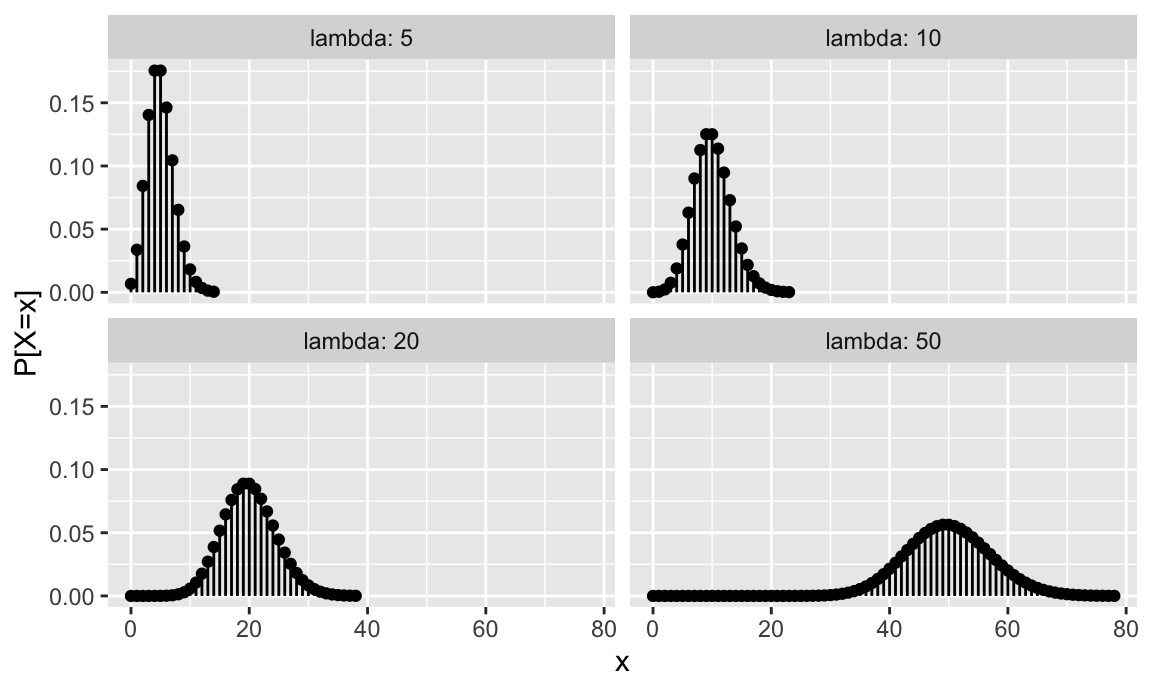
Figura 7.2: Representación de la función de probabilidad del modelo de Poisson

Las características principales de la distribución de Poisson son las siguientes:

• Media: \(\mu=E[X] = \lambda\).
• Varianza: \(\sigma^2=\mathit{V}[X] = \lambda\).

Como la binomial, también cumple la propiedad aditiva de modo que, para \(m\) variables aleatorias independientes de Poisson:

\[Y=\sum\limits_{j=1}^m {X_j},\; X_j \sim \mathit{Poiss}(\lambda_j) \implies Y \sim \mathit{Poiss}\left ( \sum\limits_{j=1}^m \lambda_j \right ).\]

En una parada de autobús llegan de media cuatro autobuses cada hora. Cuál es la probabilidad de llevar una hora y que no haya pasado ninguno todavía?

Si \(X:\) número de autobuses que pasan en una hora, entonces:

\[X \sim \mathit{Poiss}(4),\] y entonces lo que queremos saber es:

\[P[X=0]= \frac{e^{-\lambda}\lambda^x}{x!}=\frac{e^{-4}\cdot 4^0}{0!}\simeq 0.0183.\]

HOJA DE CÁLCULO

En este caso la función si es la misma en Excel y en las hojas de cálculo libres.

=POISSON.DIST(0;4;0)

R

La siguiente expresión calcula la probabilidad pedida. Nótese que ahora se utiliza pois en el nombre de la función.

dpois(x = 0, lambda = 4)
#> [1] 0.01831564

La tasa media semanal de visitas de un cliente a la página web de ofertas es igual a 8. Calcular la probabilidad de que un posible cliente acceda menos de 3 veces en una semana. En términos de variable aleatoria, tenemos que:

• \(X\): Número de visitas por semana a la web de oferta

• \(X \sim \mathit{Poiss}(8)\)

• \(P[X < 3] = P[X \leq 2] = \sum\limits_{x = 0}^2 P[X = x]=P[X=0] + P[X=1]+P[X=2]\) \(\simeq 0.0003 + 0.0027 + 0.0107=0.0138\)

Supongamos que estamos interesados en las visitas que un cliente hace a la página web durante cuatro semanas. Y queremos saber la probabilidad de que acceda 30 veces. Entonces aplicamos la propiedad aditiva de la distribución de Poisson, y definimos:

\(Y: \text{ Número de visitas en cuatro semanas } = X_1 + X_2 + X_3 + X_4,\)

donde

\(X_i: \text{ Número de visitas en el día } i, \, i = 1, 2, 3, 4 \sim \mathit{Poiss}(8)\)

Entonces:

\[Y \sim \mathit{Poiss}(32),\]

y la probabilidad buscada es:

\[P[Y = 30] = \frac{e^{-32}\cdot 32^{30}}{30!} \simeq 0.0681.\]

HOJA DE CÁLCULO

=POISSON.DIST(2;8;1)

=POISSON.DIST(30;32;0)

R

Las siguientes expresiones obtienen las probabilidades pedidas a través de la función de distribución y de probabilidad.

ppois(q = 2, lambda = 8)
#> [1] 0.01375397
dpois(x = 30, lambda = 32)
#> [1] 0.06814215

La distribución de Poisson se puede utilizar como aproximación de la distribución binomial bajo ciertas condiciones. En la práctica, para \(n\geq 100\) y \(p \leq 0.05\), se puede utilizar la aproximación:

\[X\sim \mathit{Bin}(n;\;p) \leadsto \mathit{Poiss}(\lambda=np),\] siempre y cuando \(np\) tenga sentido como parámetro \(\lambda\), es decir, no excesivamente grande ni excesivamente pequeño. La figura 7.3 muestra la función de distribución de una variable aleatoria binomial con parámetros \(n = 100, \, p = 0.05\) y su aproximación por una Poisson de parámetro \(\lambda = 5\).

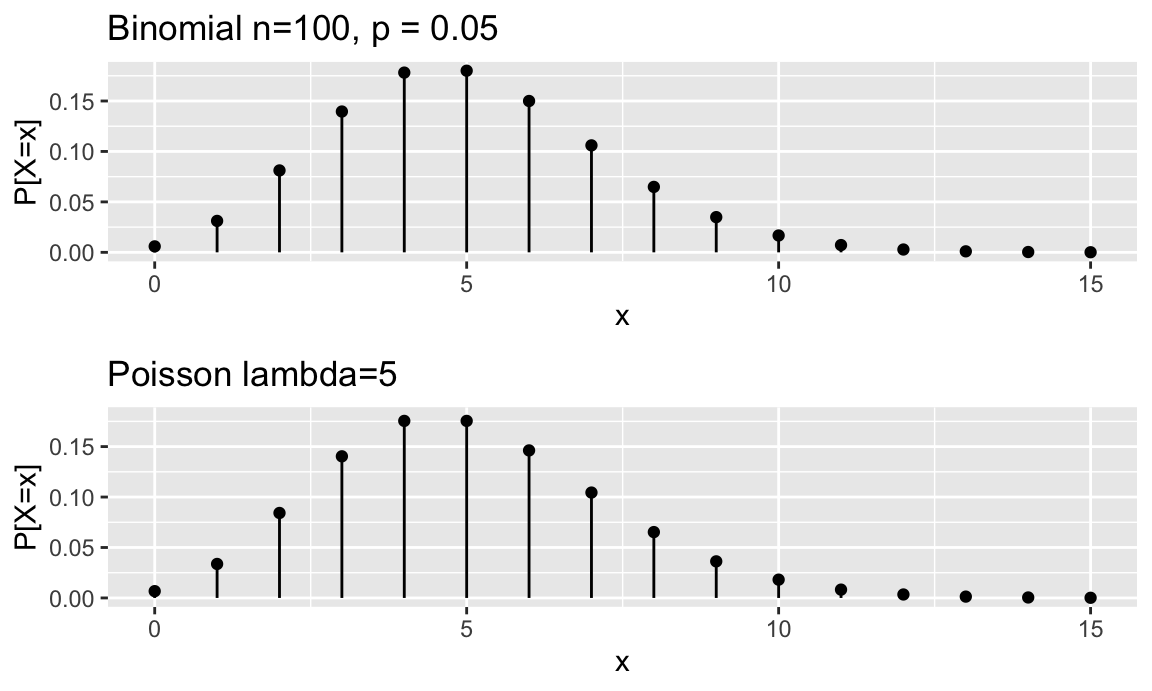
Figura 7.3: Aproximación a binomial por la Poisson

Supongamos que tenemos en la página web del estudio un formulario de contacto, y que sabemos por históricos que el 1% de los sujetos de nuestro servicio que entran al formulario, terminan enviando una reclamación.

Tomamos al azar 100 potenciales usuarios. ¿Cuál es la probabilidad de que menos de 3 hayan puesto una reclamación?

La variable aleatoria con la que podemos modelizar este problema es:

\(X: \text{ Número de clientes de una muestra de 100 que pone una reclamación},\)

que sigue una distribución binomial de parámetros \(n=100\), \(p = 0.01\). Como se dan los requisitos, podemos hacer la aproximación a la distribución de Poisson, y entonces:

\[X \leadsto \mathit{Poiss}(\lambda=1),\]

y la probabilidad pedida la podemos aproximar como:

\[P[X < 3] = \sum_{x=0}^2 \frac{e^{-1}1^x}{x!}\simeq 0.9199.\]

R

Utilizando software, podemos hacer los cálculos exactos. Vemos que, en este caso concreto, nos estaremos equivocanto en el tercer decimal.

pbinom(2, 100, 0.01)
#> [1] 0.9206268
ppois(2, 1)
#> [1] 0.9196986

7.2.4 Distribución binomial negativa

La distribución binomial negativa describe procesos en los que realizamos sucesivos experimentos independientes de Bernoulli, con probabilidad de éxito \(p\). Pero no sabemos cuántos vamos a realizar, porque lo que nos interesa es el número de fracasos \(x\) hasta que se produzcan \(c\) éxitos. También se puede expresar como el número total de pruebas necesarias \(x+c\) hasta obtener \(c\) éxitos. Así, definimos la variable aleatoria:

\[X: \text {Número de fracasos hasta } c \text{ éxitos }\]

que sigue el modelo de distribución de probabilidad binomial negativa con parámetros \(c\) y \(p\):

\[X \sim \mathit{BN}(c;\; p); \; c>0;\; 0<p<1.\]

Nótese que \(X\) puede tomar, teóricamente, cualquier valor mayor o igual que \(0\) (no tiene límite). Su función de probabilidad es:

\[\boxed{P[X = x] =\binom{x+c-1}{x}\cdot p^c \cdot (1-p)^{x};\; x = 0, 1, 2, \ldots, \infty },\]

donde:

\[\binom{x+c-1}{x}=\frac{(c+x-1)!}{x!(c-1)!}.\]

Si nos fijamos detenidamente en la función de probabilidad, podemos hacer el mismo análisis que en la binomial, multiplicando las probabilidades de cada experimento independiente de Bernoulli para una ordenación posible, y sumando las probabilidades de cada ordenación. La diferencia está en que el último experimento es siempre un éxito (habremos llegado al éxito número \(c\), y paramos). Si se da \(X=x\), entonces habremos realizado un total de \(x+c\) pruebas de Bernoulli.

El término negativa viene de la siguiente forma alternativa de escribir su función de probabilidad:

\[P[X = x] = \binom{-c}{x}\cdot p^c \cdot (1-p)^{x}.\]

La figura 7.4 muestra gráficamente la distribución de probabilidad para varios valores de \(c\) y \(p\). Se representan valores desde \(x=0\) hasta \(x= 20\). Aunque teóricamente los posibles valores son hasta infinito, a partir de cierto valor (dependiendo de los parámetros) la probabilidad es prácticamente cero. Para valores de \(p\) pequeños, esto también sucede en los valores de \(x\) bajos.

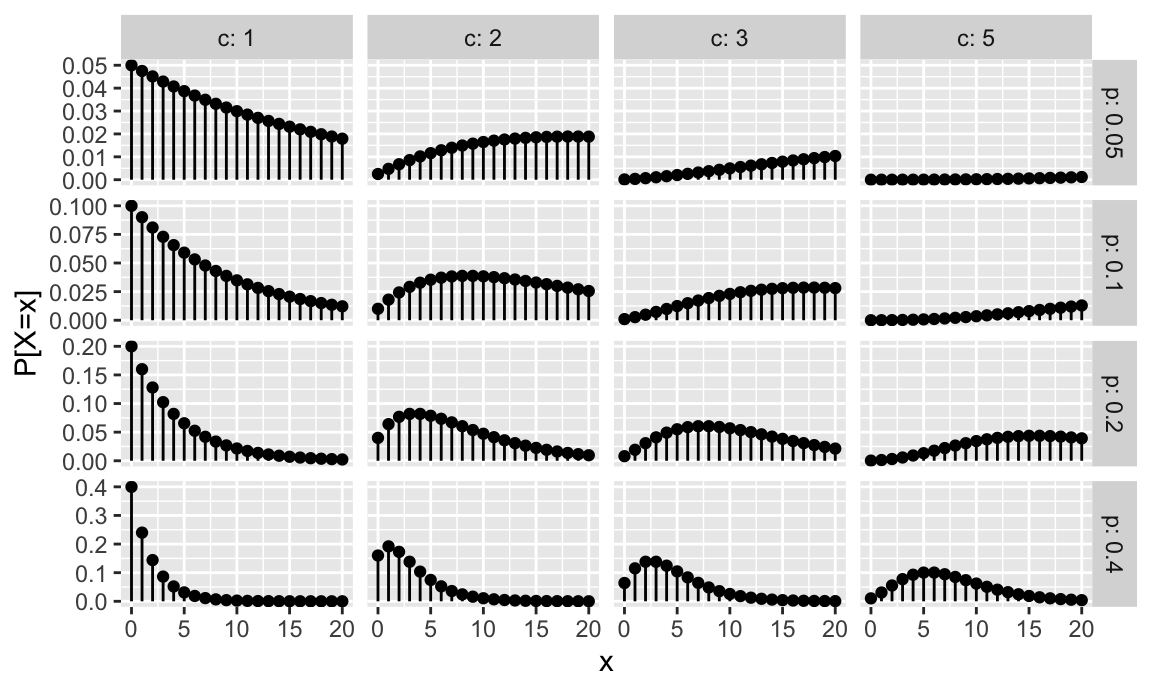
Figura 7.4: Representación de la función de probabilidad del modelo binomial negativo

La media y la varianza de una variable aleatoria que sigue un modelo binomial negativo son:

• Media: \(\mu=E[X] = \frac{c\cdot (1-p)}{p}\).
• Varianza: \(\sigma^2=\mathit{V}[X] = \frac{c\cdot (1-p)}{p^2}\).

Se cumple la propiedad aditiva de forma similar a como lo hacía en la distribución binomial. Es decir, la suma de \(m\) variables aleatorias binomiales negativas con el mismo parámetro \(p\) y parámetros \(c_j\) que pueden ser diferentes, es una variable aleatoria que sigue también una distribución binomial negativa con el mismo parámetro \(p\):

\[Y=\sum\limits_{j=1}^m {X_j},\; X_j \sim \mathit{BN}(c_j;\; p) \implies Y \sim \mathit{BN}\left ( \sum\limits_{j=1}^m c_j;\; p \right ).\]

Dos equipos de balonmano A y B se disputan la final de liga al mejor de 7 partidos. El factor campo no influye y el equipo A tiene una probabilidad de ganar un partido de \(0.6\). ¿Cuál es la probabilidad de que el equipo A gane la liga en 5 partidos?

Para plantear el problema en términos de variable aleatoria, tenemos que pensar a qué llamamos éxito y a qué llamamos fracaso, definir la variable aleatoria, y decidir cuál es el valor del que queremos calcular la probabilidad. Como la pregunta se plantea para el equipo A, que tiene una probabilidad de ganar un partido de \(0.6\), cada partido es un experimento independiente de Bernoulli con probabilidad de éxito \(p=0.6\), que vamos realizando uno tras otro. Si la liga se disputa al mejor de 7, quiere decir que la ganará el primero que gane 4. Por tanto, repetiremos el experimento de Bernoulli que hemos definido hasta tener 4 éxitos (\(c=4\)). Como el suceso que nos interesa es que el equipo A gane la partida en \(x+c=5\) partidos, esto significará que habrá perdido \(5-4=1\) partido (un fracaso). Si definimos la variable aleatoria

\(X:\) Número de partidos que pierde A antes de ganar el cuarto,

entonces

\(X\sim \mathit{BN}(c=4;\;p=0.6),\)

y por tanto buscamos la probabilidad de que pierda solo uno es la probabilidad de que la variable aleatoria sea igual a uno:

\[P[X=1]=\binom{4}{1}\cdot 0.6^4 \cdot (0.4)^{1}\simeq 0.2074.\]

HOJA DE CÁLCULO

En hojas de cálculo de Google hay que quitar el último argumento de la fórmula.

=NEGBINOM.DIST(1;4;0,6;0)

R

La siguiente expresión obtiene la probabilidad pedida.

dnbinom(x = 1, size = 4, prob = 0.6)
#> [1] 0.20736

En nuestro ejemplo ilustrativo, se seleccionan sujetos al azar y de forma independiente. ¿Cuál es la probabilidad de que se necesiten más de 10 extracciones para que haya 4 mujeres?

El experimento de Bernoulli consiste en observar si un sujeto es mujer (éxito) u hombre (fracaso). Y se repite hasta qu hayamos observado \(c=4\) mujeres. Entonces

• \(X\): Número de fracasos en pruebas independientes de Bernoulli con probabilidad de éxito 1/2 hasta el cuarto éxito

• \(X \sim \mathit{BN(4;\; 1/2)}\)

Nótese que aquí se está planteando la pregunta en términos de número total de experimentos, es decir, \(x+c > 10\), y entonces buscamos \(x > 10-4\):

\[P[X > 6] = 1- P[X \leq 6]= 1- \sum\limits_{x=0}^6 P[X=x] = \] \[ =1-(0.0625 + 0.125 + 0.1563 + 0.1562 + 0.1367 + 0.1094 + 0.082) =0.1719\]

HOJA DE CÁLCULO

=1-NEGBINOM.DIST(6;4;0,5;1)

En hojas de cálculo de Google no está el argumento para calcular acumulado, por lo que habría que calcular primero las probabilidades (desde cero hasta 6), sumar y restarlo de 1.

R

Con la siguiente expresión calculamos la probabilidad a través del complementario de la función de distribución.

pnbinom(q = 6, size = 4, prob = 0.5, lower.tail = FALSE)
#> [1] 0.171875

pnbinom(q = 6, size = 4, prob = 1/2, lower.tail = FALSE)
#> [1] 0.171875
qnbinom(p = 0.95, size = 4, prob = 1/2)
#> [1] 9

Un caso particular de la distribución binomial negativa cuando \(c=1\), es la distribución geométrica. Es decir, nos interesan el número de fracasos hasta obtener el primer éxito y entonces:

\(X\): Número de fracasos hasta obtener el primer éxito en una serie de pruebas independientes de Bernoulli con probabilidad de éxito \(p\):

\[X \sim \mathit{Ge}(p); \; 0<p<1,\] cuya función de probabilidad se simplifica bastante, ya que solo hay una ordenación posible de los éxitos y fracasos:

\[\boxed{P[X = x] = p \cdot (1-p)^{x};\; x = 0, 1, \ldots, \infty }.\]

En la figura 7.4 la primera columna se corresponde con distribuciones geométricas. La media y varianza de una distribución geométrica son:

• Media: \(\mu=E[X] = \frac{1-p}{p}.\)

• Varianza: \(\sigma^2=\mathit{V}[X] = \frac{1-p}{p^2}.\)

Observamos los sujetos que inician sesión en la página web del estudio, y nos interesa si es un investigador o no. ¿Cuál es la probabilidad de que se lleguen menos de 5 sujetos hasta que llega el primer investigador? ¿Cuál sería el número esperado de no investigadores hasta que llegue el primer investigador?

La probabilidad de éxito es \(p=4/52\), y el suceso que nos interesa se corresponde con \(x+1<5\). Entonces:

• \(X\): Número de fracasos en pruebas independientes de Bernoulli con probabilidad de éxito 4/52 hasta el primer éxito
• \(X \sim \mathit{Ge(4/52)}\)
• \(P[X < 4] = P[X \leq 3] \simeq 0.0769 + 0.071 + 0.0655 + 0.0605 \simeq 0.2739\)

A la segunda pregunta damos respuesta calculando la media:

\[\mu = \frac{1-p}{p}= \frac{1-(4/52)}{4/52}=12,\]

Es decir, en promedio el primer directivo será el número 13 (ya que 12 es el número medio de no directivos)

HOJA DE CÁLCULO

No hay una fórmula específica para la distribución geométrica, pero podemos usar la de la binomial negativa con parámetro \(c=1\).

=NEGBINOM.DIST(3;1;4/52;1)

R

La siguiente expresión obtiene la probabilidad pedida.

pgeom(q = 3, prob = 4/52)
#> [1] 0.273975

7.2.5 Distribución hipergeométrica

La distribución hipergeométrica es el equivalente a la binomial cuando las pruebas de Bernoulli no son independientes. Se asemeja a los problemas de urnas con bolas blancas y negras, o aquellos en los que realizamos muestreos sin reposición. La variable aleatoria se define en los siguientes términos: tenemos una conjunto de \(N\) elementos (por ejemplo bolas) de los cuales \(M\) son de una determinada clase \(A\) (por ejemplo blancas). Por tanto, \(N-M\) no son de la clase \(A\) (por ejemplo negras). Extraemos \(n\) elementos sin reposición de este conjunto, y lo que nos interesa es el número de elementos de la muestra que cumplen la característica. Entonces podemos definir la variable aleatoria:

\(X\): Número de elementos de la clase \(A\) obtenidos en un muestreo sin reemplazo de tamaño \(n\) de un conjunto con \(N\) elementos totales de los que \(M\) son de dicha categoría \(A\).

Que sigue una distribución geométrica de parámetros \(N\), \(M\) y \(n\).

\[X \sim \mathit{HG}(N;\; M;\; n);\;N>M;\;N\geq n.\]

La distribución hipergeométrica tiene la siguiente función de probabilidad:

\[\boxed{P[X = x] = \frac{\binom{N-M}{n-x}\cdot \binom{M}{x}}{\binom{N}{n}};\; \max{(0, n+M-N)} \leq x \leq \min{(M,n)}}.\]

La figura 7.1 muestra gráficamente la distribución de probabilidad para varios valores de \(M\) y \(n\) y \(N=20\).

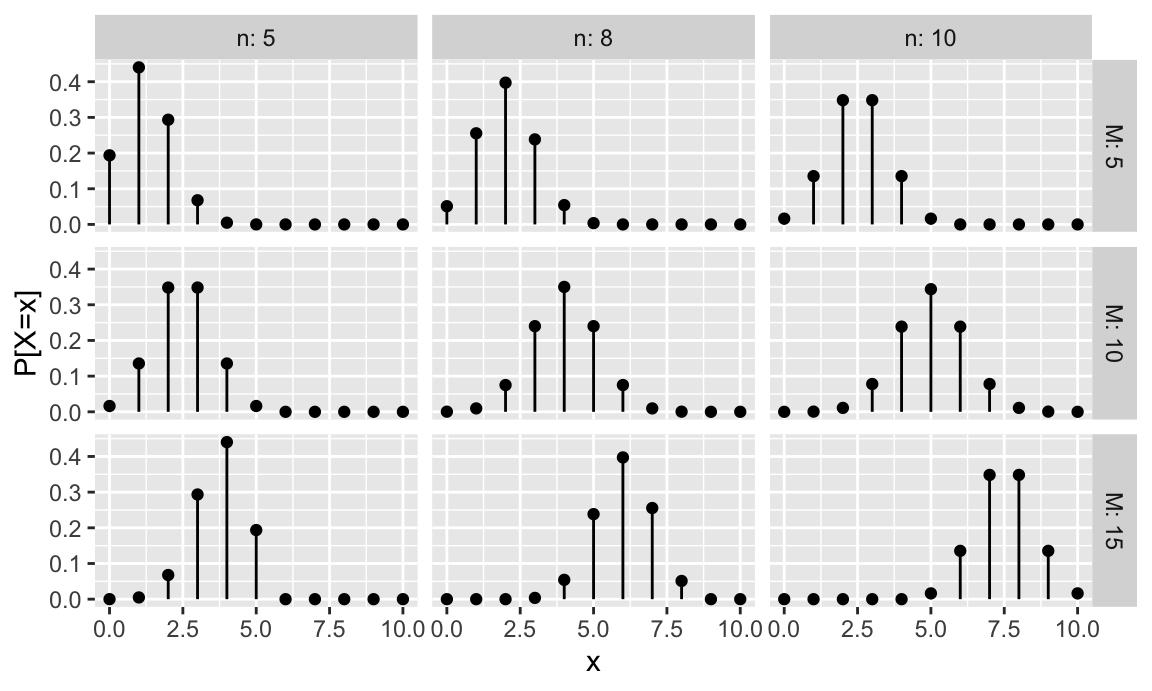
Figura 7.5: Representación de la función de probabilidad del modelo hipergeométrico

La media y la varianza de la distribución hipergeométrica son las siguientes:

• Media: \(\mu=E[X] = M\cdot \frac{n}{N}\).
• Varianza: \(\sigma^2=\mathit{V}[X] = \frac{M\cdot(N-M)\cdot n\cdot (N-n)}{N^2\cdot(N-1)}\).

Nótese que la distribución hipergeométrica no asume la independencia de los sucesivos experimentos. No obstante, es asintótica a la distribución binomial \(\mathit{Bin}\left (n;\; p = \frac{M}{N}\right)\) si \(p\) se mantiene estable. Se suele considerar apropiada la aproximación si \(\frac{n}{N}<0.1\).

En una comunidad de vecinos con 50 propietarios, 30 están de acuerdo en instalar un ascensor, y el resto no. En el descanso, cinco vecinos (al azar) se salen a fumar a la puerta. ¿Cuál es la probabilidad de que de esos cinco solo uno esté de acuerdo en instalar el ascensor?

Definimos la variable aleatoria:

\(X\): Número de vecinos de esos cinco que están de acuerdo en instalar el ascensor. Entonces:

\[X\sim \mathit{HG}(N=50;\,M=30;\,n=5),\]

y la probabilidad que buscamos es:

\[P[X=1]=\frac{\binom{50-30}{5-1}\cdot \binom{30}{1}}{\binom{50}{5}}=\frac{4845\cdot 30}{2118760}\simeq0.0686.\]

HOJA DE CÁLCULO

[EXCEL] =DISTR.HIPERGEOM.N(1;5;30;50;0)

[LibreOffice] =HYPGEOM.DIST(1;5;30;50;0)

[Hojas de Cálculo de Google] =HYPGEOM.DIST(1;5;30;50)

R

La parametrización en R es ligeramente distinta, aunque obviamente equivalente, a la que hemos usado aquí, que se corresponde con la que aparece en la definición 2.48 de la norma ISO 3534-1. Además, utiliza los términos utilizados en problemas de urnas, de forma que los argumentos de la función son:

• x: El valor (quantile) para el cual hay que calcular la probabilidad.
• m: Número de bolas blancas (white balls), que se corresponde con nuestro parámetro \(M\).
• n: Número de bolas negras (black balls), que se corresponde con \(N-M\) según nuestra parametrización.
• k: Número de bolas extraídas, que se corresponde con nuestro parámetro \(n\).

La siguiente expresión calcula la probabilidad del ejemplo.

dhyper(x = 1, m = 30, n = 20, k = 5)
#> [1] 0.06860145

Se asignan 10 premios a potenciales usuarios del servicio, pero no se pueden repetir ganadores. ¿Cuál es la probabilidad de que exactamente un directivo sea premiado?

Recordemos que teníamos 52 potenciales usuarios, de los cuales 4 eran directivos. Conocemos la composición exacta del conjunto, y es un muestreo sin reemplazamiento, por tanto la distribución adecuada es la hipergeométrica. Además, no podríamos usar la aproximación de la binomial, ya que \(10/52 \nleq 0.1\).

En términos de variable aleatoria, definimos:

\(X\): Número de directivos en una muestra sin reemplazamiento de tamaño 10 realizada sobre un conjunto de 52 personas de las que 4 son directivos.

Entonces:

• \(X \sim \mathit{HG}(N=52;\; M=4;\; n=10)\)
• \(P[X = 1]\simeq 0.4240\)

dhyper(x = 1, m = 4, n = 52-4, k = 10)
#> [1] 0.4240465

7.3 Modelos de distribución de probabilidad continuos

7.3.1 Introducción

En este apartado vamos a revisar algunas distribuciones de probabilidad continuas que tienen interés en ciencias e ingeniería. Al igual que en los modelos de distribución de probabilidad discretos, un conjunto de parámetros determinan completamente la distribución de probabilidad. Entonces tendremos la función de densidad, o la función de distribución, o ambas, en función de la variable \(x\) y también del conjunto de parámetros \(\boldsymbol{\theta}\). Entonces, para valores concretos de los parámetros, podremos calcular probabilidades o determinar las características de la variable aleatoria en estudio. Para algunas distribuciones de probabilidad se han tabulado los valores de la función de distribución o su complementario, y tradicionalmente se han utilizado estas tablas para resolver problemas de probabilidad. Actualmente se pueden realizar los cálculos con el uso de software. Por tanto, seguiremos utilizando la notación vista en el apartado 7.2 para indicar la distribución de probabilida continua que sigue la variable aleatoria \(X\):

\[X \sim \mathcal{D}\mathit{istr}(\boldsymbol{\theta}),\]

donde \(\mathcal{D}\mathit{istr}\) identifica el modelo de distribución de probabilidad, y \(\boldsymbol{\theta}\) es el vector de parámetros. Entonces las expresiones de la función de densidad y de distribución contendrán los parámetros: \(f(x|\boldsymbol{\theta})\), \(F(x|\boldsymbol{\theta})\).

En este capítulo veremos con detalle las distribuciones uniforme, exponencial y normal. Existen otros modelos de distribución de probabilidad continuos univariantes y multivariantes que se referencian al final del capítulo.

7.3.2 Distribución uniforme

La distribución uniforme se caracteriza por tener una densidad constante en un intervalo \([a, b]\). Si una variable aleatoria \(X\) sigue una distribución uniforme en el intervalo entre \(a\) y \(b\) lo expresamos así:

\[X \sim \mathit{U}(a;\; b);\; a < b;\; a, b \in \mathbb{R}.\] La función de densidad de una variable aleatoria continua que sigue un modelo uniforme tiene la siguiente función de densidad:

\[f(x) = \begin{cases} \frac{1}{b-a} & \text{si } a \leq x \leq b\\ 0 & \text{resto} \end{cases}\]

y la función de distribución se obtiene fácilmente a partir de esta:

\[F(x)=\int_a^x \frac{1}{b-a}dt=\left [ \frac{t}{b-a}\right ]_a^x = \frac{x}{b-a}- \frac{a}{b-a}=\frac{x-a}{b-a},\]

quedando en su forma completa como:

\[F(x) = \begin{cases} 0 & \text{si } x < a \\ \frac{x-a}{b-a} & \text{si } a \leq x < b\\ 1 & \text{si } x \geq b \end{cases}\]

La media y la varianza de una variable aleatoria uniforme se deducen fácilmente a partir de su función de densidad:

• Media: \(\mu=E[X] = \frac{a+b}{2}\).
• Varianza: \(\sigma^2=\mathit{V}[X] = \frac{(b-a)^2}{12}.\)

El modelo de distribución uniforme es muy útil para simular probabilidades y variables aleatorias a través de la \(U(0; 1)\). También se suele utilizar cuando conocemos el rango de valores pero no tenemos información sobre cuáles de esos valores son más probables. La figura 7.6 muestra la representación de las funciones de densidad y distribución de una variable aleatoria que sigue una distribución continua uniforme.

#> 
#> Attaching package: 'gridExtra'
#> The following object is masked from 'package:dplyr':
#> 
#>     combine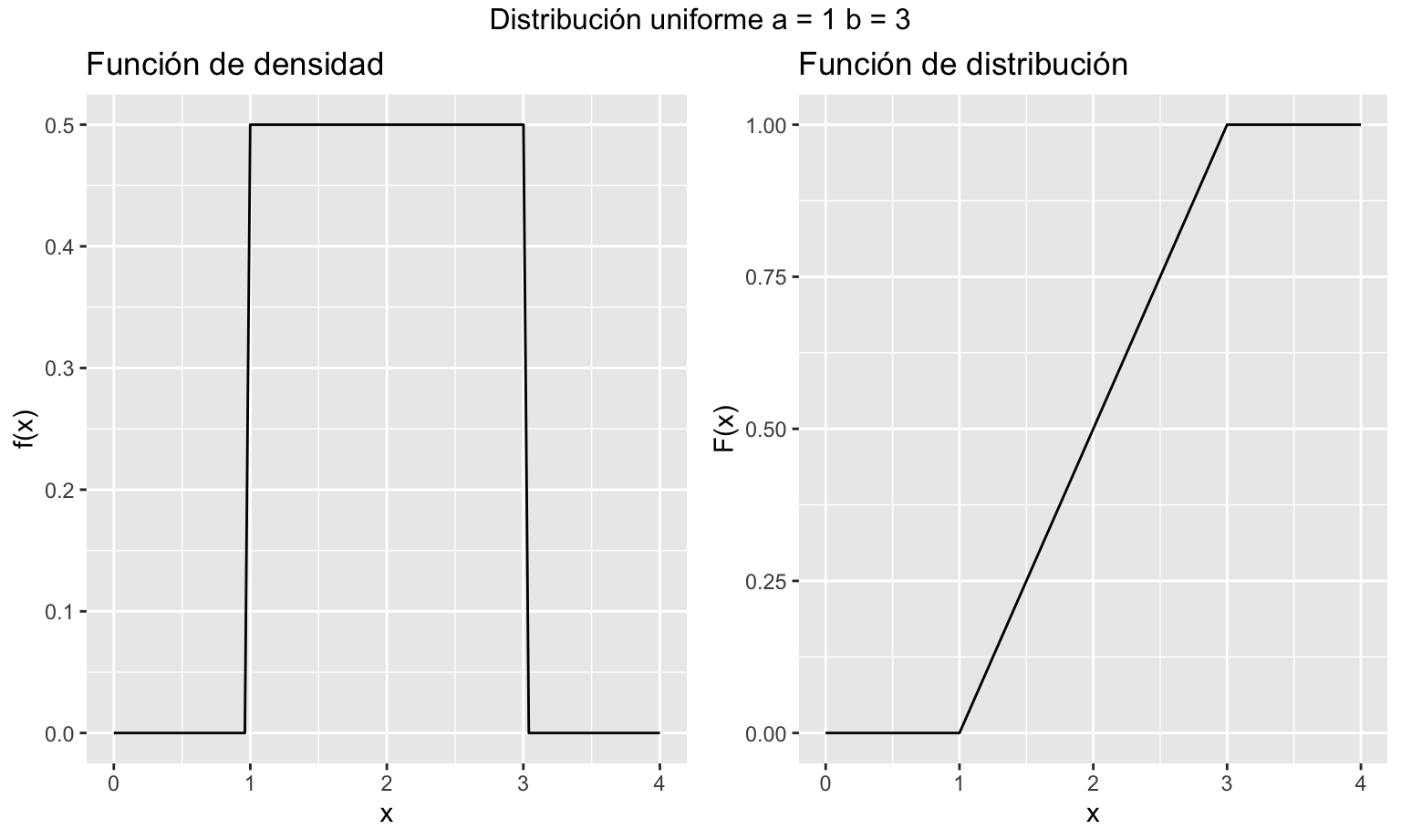

Figura 7.6: Representación gráfica de las funciones de densidad y distribución de una variable aleatoria uniforme

El volumen anual de ventas de un almacén se distribuye uniformemente entre 380 y 1200 miles de euros. ¿Cuál es la probabilidad de que las ventas sean superiores a 1000 miles de euros? ¿Cuáles son las ventas esperadas en un año?

Definimos la variable aleatoria:

\(X\): ventas del almacén un año \(X\sim U(380;\,1200)\)

Entonces la función de densidad es:

\[f(x)=\frac{1}{1200-380},\; 380<x<1200,\]

la probabilidad pedida:

\[P[X>1000]= \int_{1000}^{1200}\frac{1}{820}dx = \frac{200}{820}\simeq 0.2439.\]

Pero también podemos calcularla más fácilmente utilizando la función de distribución, que conocemos:

\[P[X>1000]= 1- P[X\leq 1000 ] = 1- F(1000) =\\= 1 - \frac{1000 - 380}{1200-380} \simeq 1 - 0.7561 \simeq 0.2439.\]

y las ventas esperadas son la media de la variable aleatoria:

\[\mu=E[X]=\frac{380+1200}{2}=790 \text{ miles de euros}.\] La figura 7.7 representa la función de densidad y la probabilidad pedida como área bajo la curva.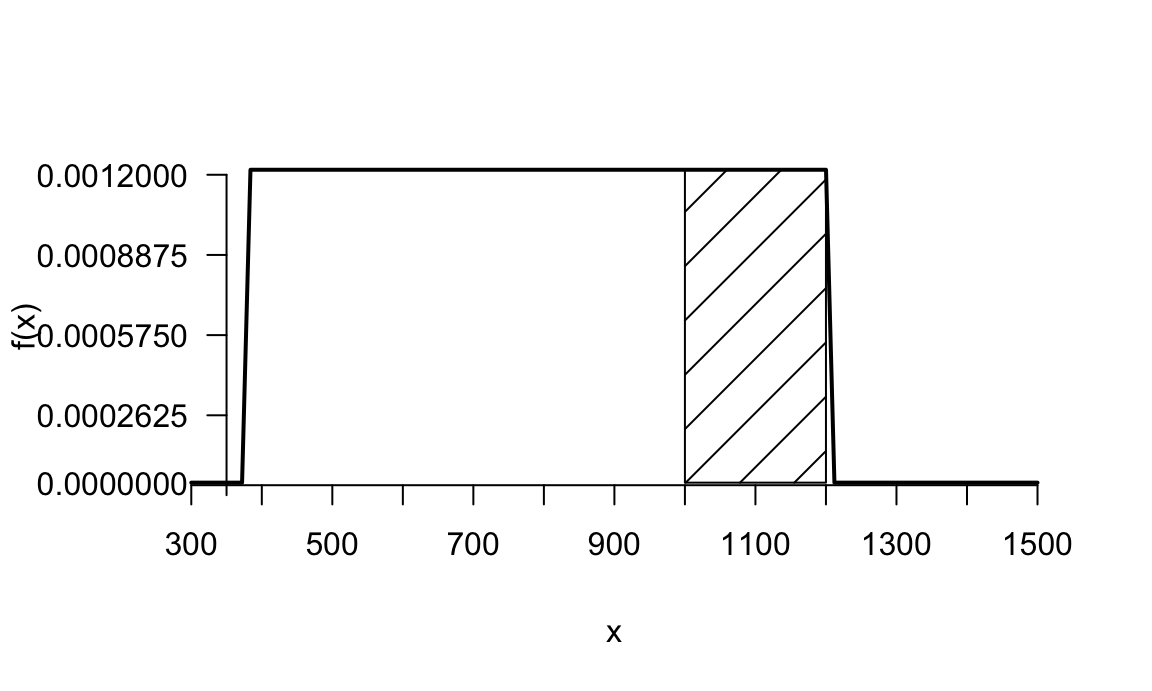

Figura 7.7: Ejemplo distribución uniforme

HOJA DE CÁLCULO

No hay funciones específicas para obtener la probabilidad de una variable aleatoria uniforme, aunque se puede insertar una fórmula con la función de distribución y a partir de ahí calcular probabilidades, por ejemplo, si en la celda A1 tenemos el valor 1000, en la celda A2 el parámetro a = 380 y en la celda A3 el parámetro b = 1200, entonces en otra celda podemos calcular la probabilidad del ejemplo como:

= 1 - (A1 - A2)/(A3 - A2)

R

La función punif devuelve la función de distribución uniforme.

punif(q = 1000, min = 380, max = 1200, lower.tail = FALSE)
#> [1] 0.2439024

Si la proporción de video visualizado por un sujeto que sigue el mensaje se distribuye de forma uniforme, ¿cuál es la probabilidad de que un visitante de la web del estudio vea más del 90% del vídeo?

En términos de variable aleatoria:

\(X\): Proporción de video visualizado, \(X \sim U(0;\; 1)\).

Entonces:

\[P[X > 0.9]=\int_{0.9}^{1}dx = 0.1.\]

O bien:

\[P[X > 0.9]=1-F(0.9)=1-\frac{0.9 - 0}{1-0} = 0.1.\]

R

Análogamente al ejemplo anterior:

punif(q = 0.9, min = 0, max = 1, lower.tail = FALSE)
#> [1] 0.1

7.3.3 Distribución exponencial

Cuando en un proceso de Poisson observamos el tiempo que transcurre entre un evento y otro, aparece la distribución exponencial. También modeliza bien tiempos de vida, por ejemplo de componentes electrónicos. La distribución exponencial solo tiene un parámetro:

\[X \sim \mathit{Exp}(\beta),\; \beta>0.\]

El parámetro \(\beta\) del modelo de distribución exponencial representa, al igual que en la distribución de Poisson, la tasa media de eventos por unidad de tiempo. Una variable aleatoria que sigue un modelo de distribución exponencial tiene la siguiente función de densidad:

\[f(x) = \begin{cases} \beta e^{-\beta x} & \text{si } x > 0\\ 0 & \text{si } x\leq 0 \end{cases}\]

La función de distribución se obtiene fácilmente a partir de la función de densidad:

\[F(x)=\int_{-\infty}^xf(t)dt=1-e^{-\beta x}, \; x > 0.\]

La figura 7.8 muestra la representación de las funciones de densidad y distribución de una variable aleatoria que sigue una distribución continua exponencial.

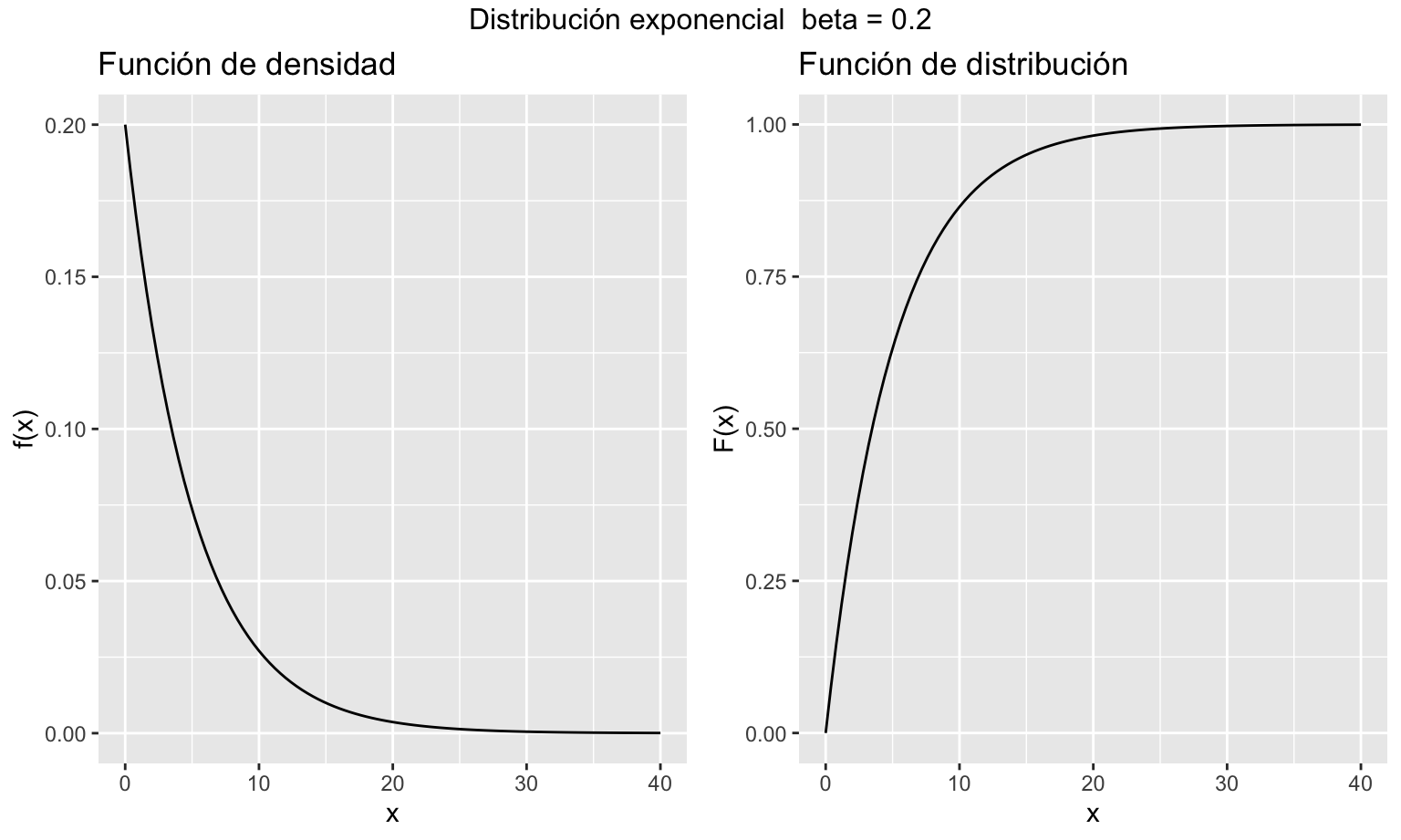
Figura 7.8: Representación gráfica de las funciones de densidad y distribución de una variable aleatoria exponencial

La media y la varianza de una variable aleatoria que sigue el modelo exponencial son:

• Media: \(\mu=E[X] = \frac{1}{\beta}\).
• Varianza: \(\mathit{V}[X] = \frac{1}{\beta^2}.\)

Se dice que la exponencial es una variable aleatoria sin memoria, en el sentido de que el tiempo que haya tardado en ocurrir un evento, es independiente de cuándo sucedió el anterior:

\[(P[X > t_2 + t_1 | X > t_1] = P[X > t_2]).\]

La distribución exponencial es un caso particular de la distribución gamma, que no vemos en este texto. La distribución gamma modeliza el tiempo transcurrido hasta ocurrir un número determinado de eventos.

El tiempo en horas que se tarda en arreglar una máquina sigue una distribución exponencial de parámetro \(\beta=4\). ¿Cuál es la probabilidad de que una avería tarde más de una hora en ser reparada?

\[X\sim \mathit{Exp}(4),\]

\[P[X>1]=1-\int_0^14 e^{-4x}dx=1-\left[-e^{-4x}\right]_0^1=1-(-e^{-4}-(-e^0))=e^{-4}\simeq 0.0183.\]

Es más sencillo si lo resolvemos con la función de distribución:

\[P[X>1]=1-F(1)=1-(1-e^{-4\cdot 1})=\simeq 0.0183.\]

La figura 7.9 muestra la representaciń gráfica de la función de densidad del ejemplo.

HOJA DE CÁLCULO

[EXCEL] =1-DISTR.EXP.N(1; 4; 1)

[LibreOffice] =1-EXPON.DIST(1;4;1)

R

La función pexp obtiene la función de distribución del modelo exponencial.

pexp(q = 1, rate = 4,lower.tail = FALSE)
#> [1] 0.01831564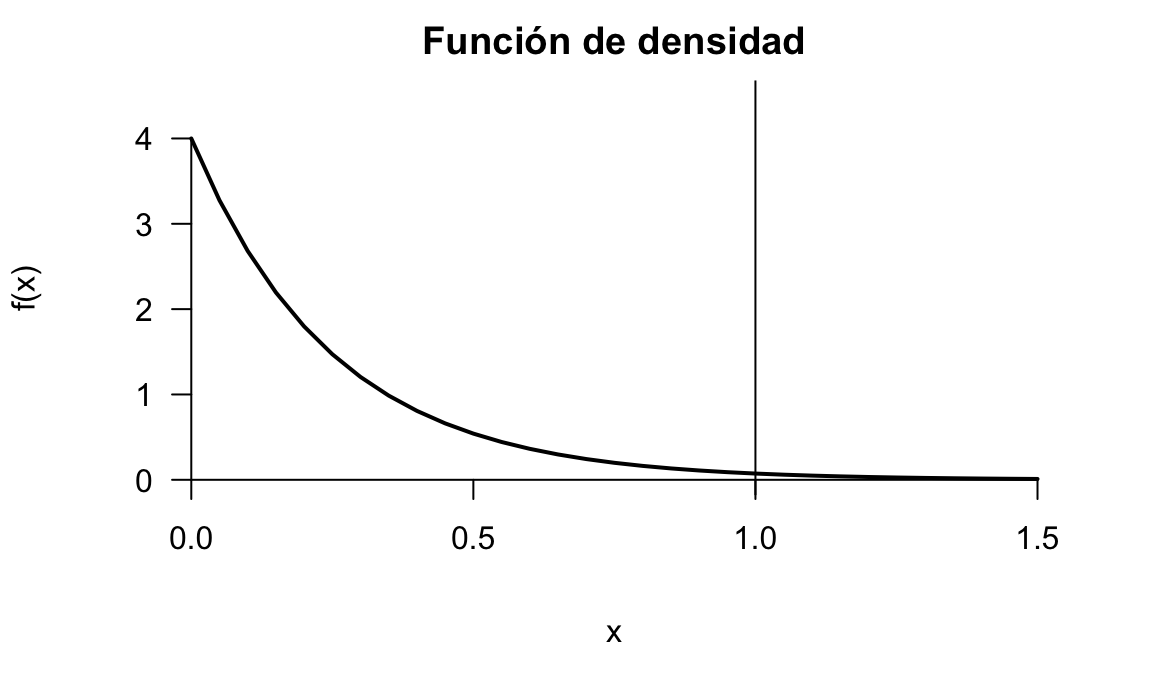

Figura 7.9: Representación de la función de densidad del modelo exponencial del ejemplo

En ocasiones nos interesa calcular la inversa de la función de distribución. Es decir, encontrar un valor de la variable aleatoria para el cual se cumple alguna condición de probabilidad, como en el siguiente ejemplo.

El tiempo que permanece un visitante en la web del estudio sigue una distribución exponencial. La tasa media de abandonos es de 2 cada minuto. ¿Cuánto tiempo permanece como máximo el 95% de los usuarios antes de abandonar?

En términos de variable aleatoria:

\(X\): Tiempo hasta abandonar la web tras hacer clic en el mensaje, \(X\sim \mathit{Exp}(2)\).

En este caso, lo que nos interesa es obtener el cuantil 0.95, es decir, el valor \(x\) de la variable aleatoria para el cual \(P[X > x] = 0.05\), o lo que es lo mismo, \(P[X \leq x]=0.95\). como tenemos la expresión de la función de distribución, no hay más que despejar y tenemos:

\[F(x) = 0.95 \iff 1-e^{-2x}=0.95 \iff x = 1.498 \text{ minutos}.\]

También nos podemos preguntar cuánto tiempo permanece un visitante, en promedio, en la web. Entonce calculamos la experanza:

\[\mu = \frac{1}{\beta} = 0.5\]

R

La función qexp obtiene la inversa de la función de distribución del modelo exponencial.

qexp(p = 0.95, rate = 2)
#> [1] 1.497866

7.3.4 Distribución normal

Sin duda, la distribución normal (o gaussiana) es el modelo de distribución de probabilidad continuo más importante de todos. Gracias al teorema central del límite que veremos en el capítulo 7.5, muchas situaciones se aproximan a la distribución normal⁶⁷. El modelo de distribución normal queda determinado por dos parámetros, que son su media \(\mu\) y su desviación típica \(\sigma\):

\[X \sim \mathit{N}(\mu;\; \sigma);\; \mu \in \mathbb{R}, \sigma > 0.\]

La función de densidad de una variable aleatoria que sigue el modelo de distribución normal tiene la siguiente función de densidad:

\[f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}},\;-\infty < x < \infty.\]

La figura 7.10 muestra la función de densidad y la función de distribución para unos valores determinados de \(\sigma\) y \(\mu\). La función de distribución se ha obtenido por métodos numéricos, ya que no es posible obtener una expresión analítica de \(F(x)\) al no existir una primitiva de \(f(x)\).

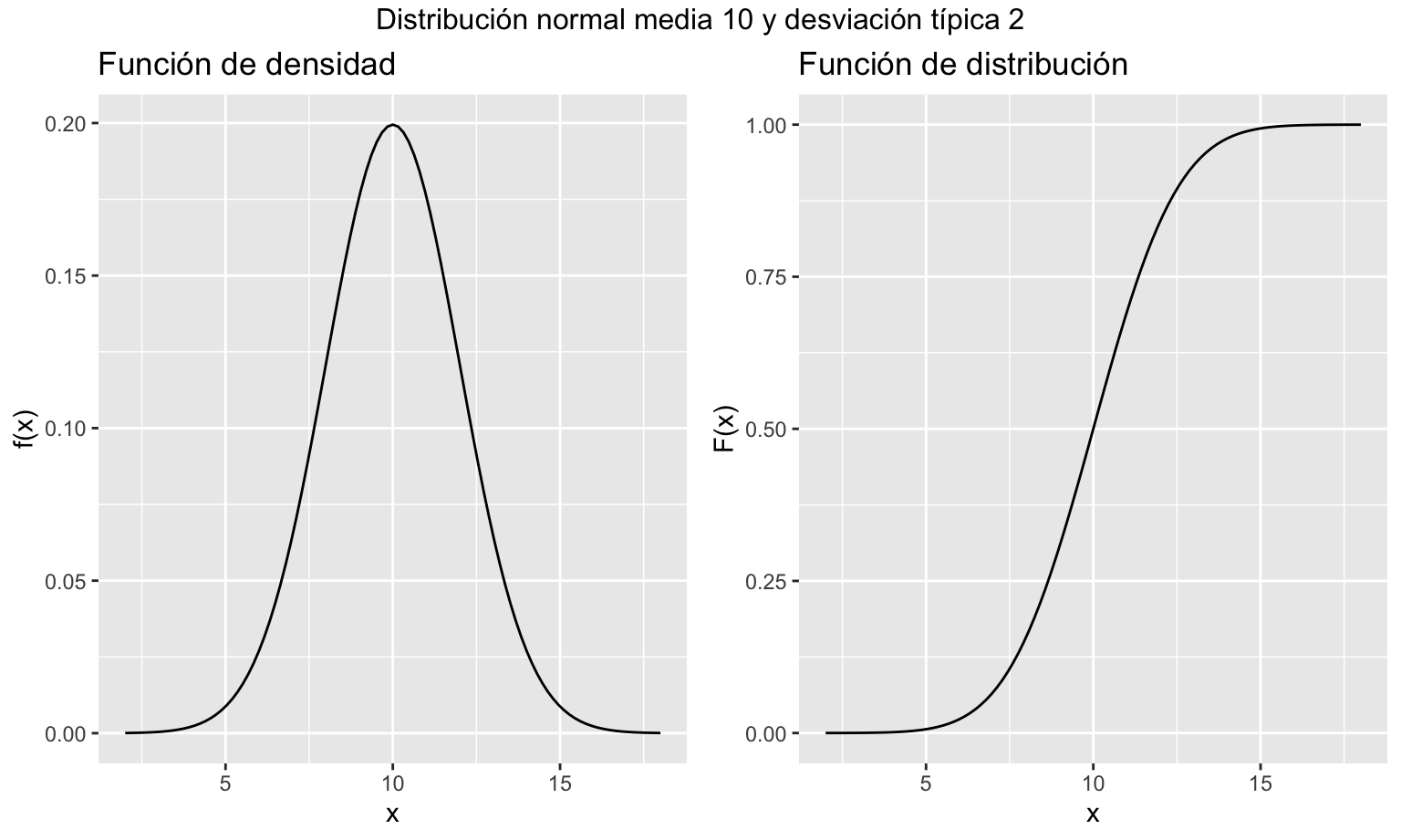
Figura 7.10: Representación gráfica de las funciones de densidad y distribución de una variable aleatoria normal

La distribución normal es simétrica respecto de la media, siendo la mediana y la moda igual a ella. Esta importante propiedad implica que \(P[X \leq \mu] = 0.5\). Cuanto más cerca de la media estén los valores, más probables son, y a medida que nos alejamos de la media, cada vez son más improbables, de hecho como vemos en la figura 7.11 entre la media y dos desviaciones típicas tenemos más del 95% de la probabilidad, y la probabilidad de que la variable aleatoria tome valores más allá de tres desviaciones típicas desde la media es de solo 0.0027. La función de densidad presenta puntos de inflexión en \(\mu \pm \sigma\).

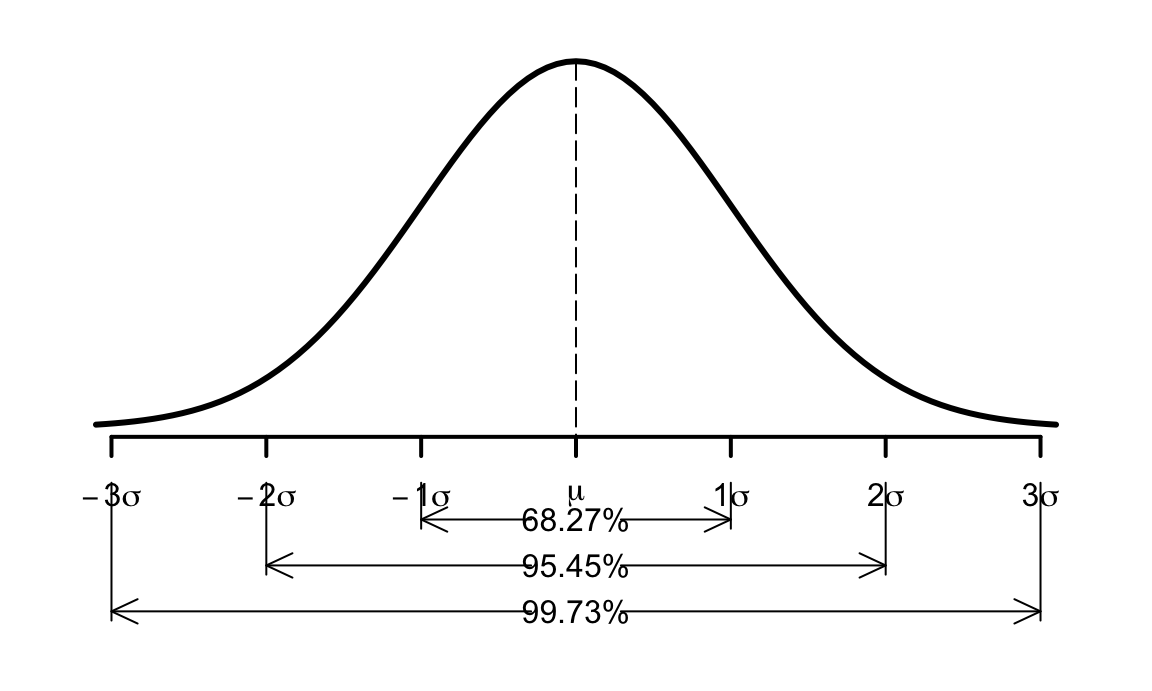
Figura 7.11: Función de densidad de la distribución normal

El modelo de distribución normal cumple la propiedad aditiva, de modo que si tenemos las variables aleatorias:

\[X_j \sim N(\mu_j; \sigma_j) \; \forall\; j=1, \ldots, n,\]

entonces la variable aleatoria:

\[Y=a+\sum\limits_{j=1}^n b_j X_j,\] no siendo todos los \(b_j\) nulos, se distribuye también como una distribución normal, y por tanto por las propiedadades de la esperanza y la varianza que vimos en el capítulo 5:

\[Y \sim N\left(a+\sum\limits_{j=1}^n b_j \mu_j; \sqrt{\sum\limits_{j=1}^n b_j^2 \sigma_j^2} \right ).\]

Un caso particular del modelo de distribución normal, es la distribución normal estándar, cuyos parámetros serán \(\mu=0\) y \(\sigma=1\), y que vamos a representar en este texto como \(Z\)⁶⁸:

\[Z \sim N(0;1).\] La función de densidad en este caso quedaría:

\[f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}},\;-\infty < x < \infty.\]

Nótese que, al ser la distribución normal simétrica, se cumple que \(P[Z \leq 0] = 0.5\).

Trabajar con variables aleatorias estandarizadas es conveniente en muchas situaciones. En particular, se ha utilizado tradicionalmente para obtener probabilidades por medio de tablas estadísticas que contienen probabilidades de la distribución normal estandarizada, bien la función de distribución \(F(z)=P[Z \leq z]\) o su complementario \(P[Z>z]\). A través de estas tablas podemos hacer cálculo de probabilidades para cualquier variable aleatoria normal, con cualesquiera \(\mu\) y \(\sigma\), ya que se cumple, según la aditividad y las propiedades de la esperanza y la varianza:

\[X \sim N(\mu;\; \sigma) \implies Z = \frac{X-\mu}{\sigma} \sim N(0;\;1).\] Ya vimos en el capítulo 5 que podemos estandarizar cualquier variable aleatoria. Si estandarizamos una distribución normal con cualesquiera parámetros \(\mu\) y \(\sigma\), entonces tendremos variables aleatorias estandarizadas.

A la hora de calcular probabilidades de la distribución normal, nos encontramos que la función de densidad no es integrable, es decir, no podemos encontrar una primitiva. Entonces, en vez de utilizar integrales se utilizan métodos numéricos o tablas como se ha descrito anteriormente.

El procedimiento para calcular probabilidades de variables aleatorias que siguen el modelo de distribución normal es el siguiente:

1. Determinar los parámetros de la distribución \(\mu\) y \(\sigma\) (para el alcance de este capítulo, vendrán dados).

2. Tipificar el/los valores de la variable \(X\) para los que se quiere calcular la probabilidad (\(X \to Z\)).

3. Utilizando las propiedades de la probabilidad, transformar la expresión de la probabilidad que se quiere calcular en expresiones compatibles con la tabla a utilizar, por ejemplo \(P[Z\leq z]\)

4. Buscar dentro de la tabla las probabilidades que se necesiten para los valores \(z\) y hacer los cálculos.

Para la operación inversa del cálculo de cuantiles a partir de una probabilidad, procedemos de la siguiente forma:

1. Tipificar la variable aleatoria, obteniendo una expresión \(z=\frac{x-\mu}{\sigma}\), donde \(x\) es el valor que queremos encontrar.

2. Expresar la probabilidad en forma compatible con la tabla a utilizar, por ejemplo \(P\left [Z\leq\frac{x-\mu}{\sigma}\right ]=p\).

3. Buscar dentro la tabla la probabilidad deseada \(p\).

4. Encontrar el valor de \(z\) que se corresponde con dicha probabilidad, y despejar \(x\) de la expresión \(z=\frac{x-\mu}{\sigma}\).

En lo que sigue, utilizaremos la tabla de la cola inferior de la distribución normal estandarizada, disponible en el apéndice C. En esta tabla tenemos, para valores de \(z>0\), \(P[Z \leq z]\). Con estos valores, seremos capaces de calcular cualquier probabilidad utilizando las siguientes propiedades y gracias a la simetría de la distribución. Dados \(a < b\) positivos, debemos expresar cualquier probabilidad de forma que podamos buscarla en la tabla:

• En la tabla tenemos \(P[Z \leq b]\) o \(P[Z \leq a]\).

• \(P[Z > a] = P[Z \leq -a] = 1- P[Z \leq a]\).

• \(P[Z > -a] = P[Z \leq a]\).

• \(P[-b \leq Z\leq -a]\) = \(P[a \leq Z \leq b]= P[Z \leq b] - P[Z \leq a]\).

• \(P[-a \leq Z\leq b]\) = \(P[Z \leq b] + P[Z \leq a] - 1\).

La figura 7.12 resume estos cálculos. Ayudará al lector pensar en la probabilidad en términos de área bajo la curva de la función de densidad, teniendo en cuenta que el área total debe ser igual a la unidad, y que el área por encima y por debajo de cero es \(0.5\). La misma lógica se aplicaría en el caso de utilizar una tabla con la cola superior que podamos encontrar en alguna otra bibliografía.

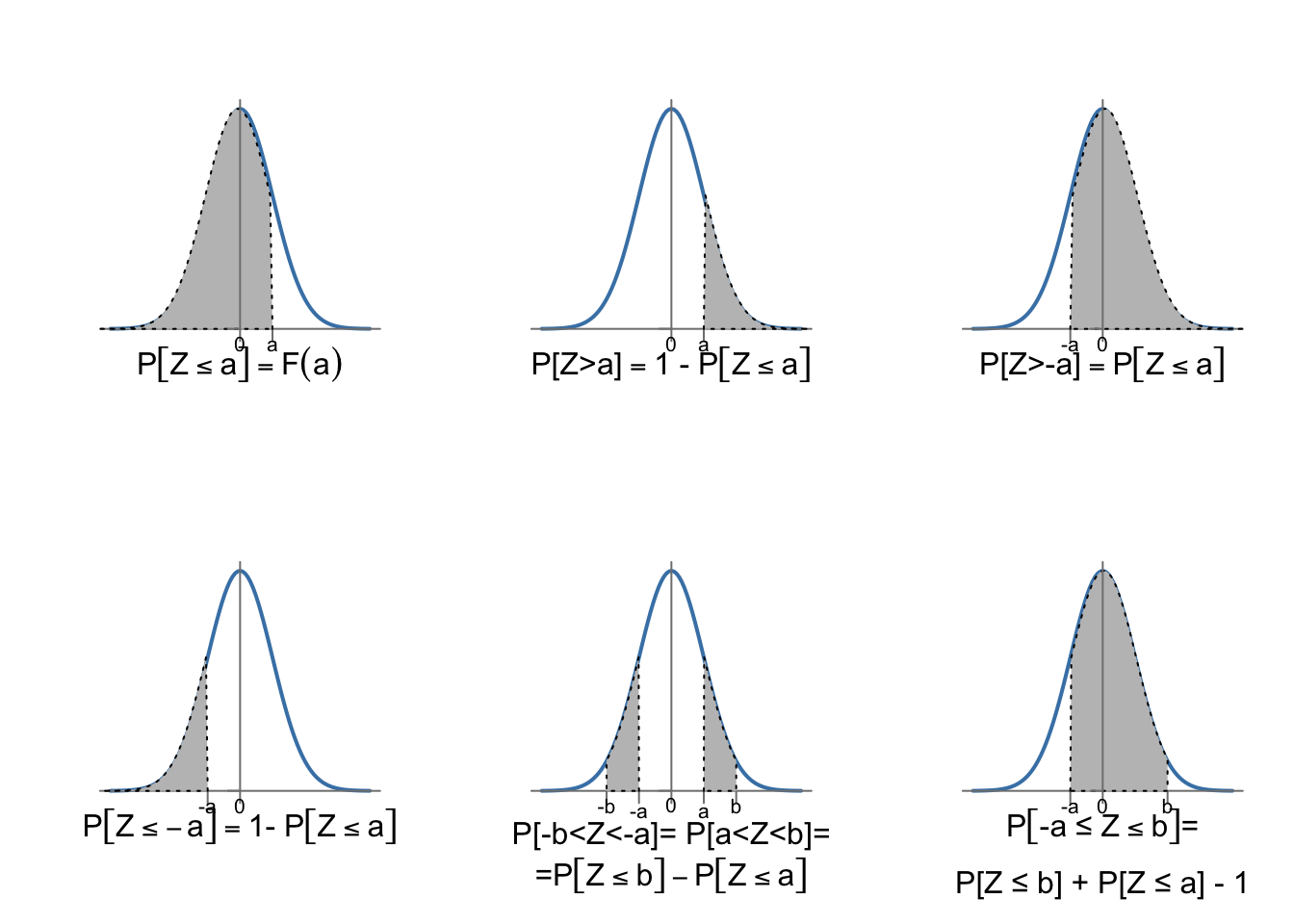
Figura 7.12: Cálculo de probabilidades de la distribución \(N(0; 1)\)

En un curso de reciclaje dirigido a teleoperadores las puntuaciones obtenidas en el test final se distribuyen siguiendo un modelo normal de media 5 y desviación típica 2. Con menos de tres puntos un teleoperador no promociona. ¿Cuál es la probabilidad de que un teleoperador no promocione? ¿Cuál es la puntuación mínima que han obtenido el 3% de los teleoperadores mejor preparados?

La variable aleatoria es:

\(X:\) Calificación obtenida por el teleoperador, \(\sim N(5; 2)\),

y lo que buscamos es la probabilidad de obtener menos de tres puntos:

\[P[X<3]=P\left[\frac{X-5}{2}<\frac{3-5}{2} \right]=P[Z < -1]=1-P[Z\leq 1]=\boxed{0.1587}.\]

A la segunda pregunta contestamos de manera inversa. Tenemos una probabilidad \(p=0.03\), y buscamos el valor \(x\) de la variable que cumple:

\[P[X\leq x] = 1- 0.03,\] o lo que es lo mismo:

\[P\left [Z\leq\frac{x-\mu}{\sigma}\right] = 0.97,\]

Buscamos esta probabilidad en el interior de la tabla⁶⁹, en este caso el valor más próximo redondeando a dos decimales es \(0.9699\), que se corresponde con un valor \(z=1.88\). Entonces tenemos:

\[z=\frac{x-\mu}{\sigma} \iff 1.88=\frac{x-5}{2} \iff x = 1.88\cdot 2 + 5=\boxed{8.76},\]

Es decir,

\[P[X>8.76]\simeq 0.03.\]

La figura 7.13 representa gráficamente los dos cálculos realizados.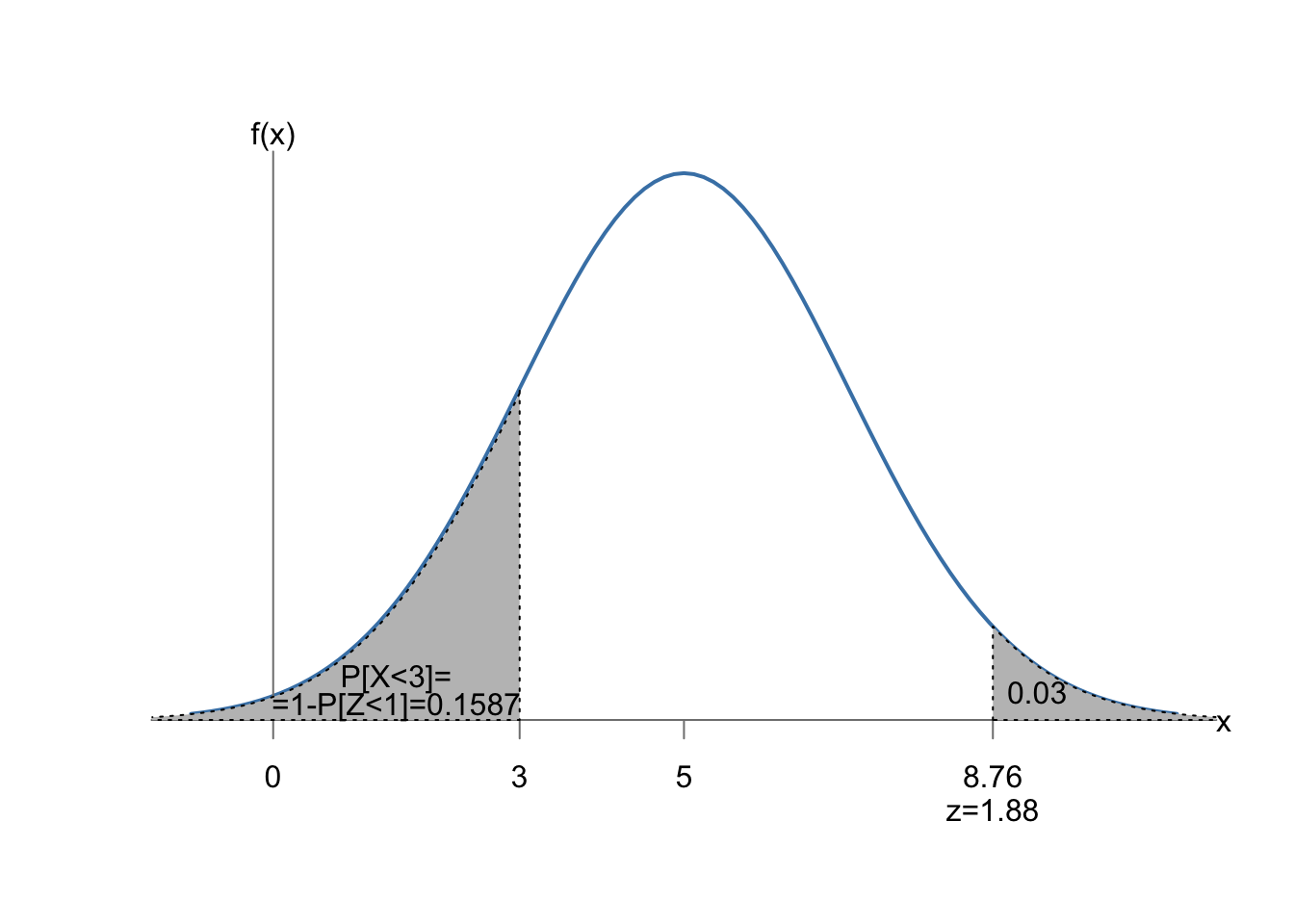

Figura 7.13: Ejemplo de cálculo de probabilidad y cuantil de la normal

Al utilizar software, no es necesario estandarizar. Le pasaremos directamente los parámetros de la distribución normal a la función correspondiente.

HOJA DE CÁLCULO

[LibreOffice] =NORM.DIST(3;5;2;1)

[EXCEL] =DISTR.NORM.N(3;5;2;1)

Para obtener el cuantil, tenemos que pasar como argumento de probabilidad 1-0.03, ya que siempre da la cola inferior.

[LibreOffice] =NORM.INV(0,97;5;2)

[EXCEL] =INV.NORM(0,97;5;2)

R

Con la función pnorm calculamos la probabilidad, y con la función qnorm, el cuantil.

pnorm(q = 3, mean = 5, sd = 2)
#> [1] 0.1586553
qnorm(p = 0.03, mean = 5, sd = 2, lower.tail = FALSE)
#> [1] 8.761587

El peso de los paquetes que contienen los pedidos que recibe un laboratorio se distribuye según una distribución normal de media \(1.8\) y desviación típica \(0.5\) kg. ¿Cuál es la probabilidad de que un paquete esté entre 1 y 2 kilos?

Definimos la variable aleatoria:

\(X:\) Peso de los paquetes, \(X\sim N(1.8, 0.5)\).

Entonces:

\[P[1 \leq X \leq 2] = P \left [\frac{1-1.8}{0.5} \leq \frac{X-\mu}{\sigma} \leq \frac{2-1.8}{0.5} \right ] = \] \[=P[-1.6 \leq Z \leq 0.4] =P[Z\leq 0.4]-P[Z\leq -1.6]=\] \[P[Z\leq 0.4]-(1-P[Z\leq 1.6])=0.6554+0.9452-1=\boxed{0.6006}.\]

¿Por debajo de qué peso estarán probablemente al menos el 95% de los paquetes?

Buscamos el valor de \(x\) que cumpla:

\[P[X<x] = 0.95\]

Buscamos esta probabilidad en el interior de la tabla, y hay dos valores que nos servirían si redondeamos a dos decimales: \(0.9495\), correspondiente a \(z=1.64\) y \(0.9505\), correspondiente a \(z=1.65\). Vamos a tomar este último para asegurarnos la probabilidad de \(0.95\)⁷⁰. Solo nos queda igualar este valor a la \(x\) estandarizada y depejar:

\[z=\frac{x-\mu}{\sigma} \iff 1.65=\frac{x-1.8}{0.5} \iff x = 1.65\cdot 0.5 + 1.8=2.625.\]

Entonces, el 95% de los paquetes pesan más de \(2.625\) kg.

Resolvemos de forma análoga al ejemplo anterior. Nótese cómo ahora calculamos el cuantil exacto para la probabilidad de 0.95. Como las funciones nos dan la función de distribución, aplicamos que \(P[a \leq x < b] = F(b)- F(a)\).

HOJA DE CÁLCULO

[LibreOffice] =NORM.DIST(2;1,8;0,5;1) - NORM.DIST(1;1,8;0,5;1)

[LibreOffice] =NORM.INV(0,95;1,8;0,5)

[EXCEL] =DISTR.NORM.N(2;1,8;0,5;1) - DISTR.NORM.N(1;1,8;0,5;1)

[EXCEL] =INV.NORM(0,95;1,8;0,5)

R

pnorm(2, 1.8, 0.5) - pnorm(1, 1.8, 0.5)
#> [1] 0.6006224
qnorm(p = 0.95, 1.8, 0.5)
#> [1] 2.622427

7.3.5 Mezcla de poblaciones y adición de variables aleatorias

Vamos a ilustrar con un ejemplo más completo la propiedad de la aditividad de variables aleatorias normales. Es importante no confundir la aditividad con la mezcla de poblaciones. En ambos casos el problema al que nos enfrentamos puede estar referido a una característica que se observa en dos grupos, y a veces es difícil distinguir si tenemos que resolverlo mediante la probabilidad total y el teorema de Bayes, o mediante la suma de variables aleatorias. Para diferenciarlo, debemos entender bien el planteamiento del problema. Algunos indicios que nos ayudarán son:

• Mezcla de poblaciones: Hay dos o más grupos en los que se observan elementos tomados al azar. La característica tiene distinta distribución de probabilidad en cada grupo, pero la probabilidad de interés se refiere a las poblaciones mezcladas (probabilidad total) o a la probabilidad de pertenecer a uno de los grupos, condicionado a que se ha producido algún evento de interés.

• Suma de variables aleatorias: Hay dos o más variables aleatorias (que se pueden referir a grupos distintos, y de ahí la posible confusión con la mezcla de poblaciones). Pero lo que nos interesa es estudiar la variable aleatoria que resulta de hacer operaciones con esas variables aleatorias (por ejemplo, sumarlas).

En el siguiente ejemplo se plantean preguntas que abordan los dos problemas.

Una empresa de comercio minorista tiene tres tiendas (A, B y C) en una determinada ciudad. El tiempo que se tarda en atender a un cliente se distribuye según una distribución exponencial de media 2 minutos, 4 minutos y 5 minutos en las tiendas A, B y C respectivamente. La tienda C atiende a tantos clientes como A y B juntas (que atienden al mismo número de clientes). Si llamamos \(T_A\), \(T_B\), \(T_C\) a las variables aleatorias “tiempo en ser atendido en la tienda A, B, o C” respectivamente, entonces:

\[T_A \sim \mathit{Exp}(0.5),\] \[T_B \sim \mathit{Exp}(0.25),\] \[T_C \sim \mathit{Exp}(0.2).\]

Se considera que un cliente estará insatisfecho si se tarda más de 8 minutos en atenderle.

Por otra parte, las ventas diarias de cada tienda, \(V_A\), \(V_B\) y \(V_C\), son independientes, y se distribuyen según una distribución normal con los siguientes parámetros en miles de unidades monetarias (u.m.):

\[V_A \sim N(\mu = 100; \sigma = 10),\] \[V_B \sim N(\mu = 150; \sigma = 20),\] \[V_C \sim N(\mu = 140; \sigma = 40).\]

Cuestion 1:

1. ¿Cuál es la probabilidad de que un cliente de la empresa no esté satisfecho con el tiempo de servicio?
2. Recibimos una queja de un cliente insatisfecho con el tiempo de servicio. ¿Cuál es la probabilidad de que sea un cliente de la tienda A?

Cuestión 2:

Las tiendas A y B son propiedad 100% de la empresa. Pero de la tienda C la empresa realmente solo recauda el 50%, ya que el otro 50% es de otro socio. Por otra parte, la empresa recibe unos ingresos fijos de 25.000 u.m. diarios de una tienda franquiciada en otra ciudad.

1. ¿Qué distribución de probabilidad siguen las ventas totales de la empresa, teniendo en cuenta su participación en las tiendas?

2. ¿Cuál es la probabilidad de que un día cualquiera esas ventas totales sea de menos de 300.000 u.m.?

Para resolver cada cuestión, tenemos que pensar si estamos anta una mezcla de poblaciones, o una suma de variables. Al estar los dos problemas planteados, es fácil de ver. Pero si solamente nos estuvieran preguntando por una de las dos cosas, pueden surgir dudas.

La primera cuestión es un típico problema de probabilidad total y Teorema de Bayes en el que tenemos una partición del espacio muestral en tres tiendas, y conocemos las probabilidades a priori. En cuanto al suceso de interés (cliente insatisfecho), conocemos las distribuciones de probabilidad de cada tienda, y tendremos que calcular las probabilidades condicionadas a cada tienda.

En la segunda cuestión lo que tenemos es una combinación lineal de variables aleatorias, porque las ventas totales serán la suma de las ventas de las tiendas. Además, una de las variables estará multiplicada por un coeficiente, y tenemos también una constante que sumar.

Pasemos entonces a resolver cada cuestión.

Cuestión 1.a)

Consideremos el suceso \(D\): el cliente está insatisfecho (espera más de 8 minutos). Entonces buscamo \(P(D)\). En la definición del problema tenemos las distribuciones de probabilidad del tiempo de espera, entonces podemos calcular:

\[P(D|A) = P[T_A > 8] = 1 - F_{T_A}(8) = 1 - (1 - e^{-0.5\cdot 8}) \simeq 0.0183,\] \[P(D|B) = P[T_B > 8] = 1 - F_{T_B}(8) = 1 - (1 - e^{-0.25\cdot 8}) \simeq 0.1353,\] \[P(D|C) = P[T_C > 8] = 1 - F_{T_C}(8) = 1 - (1 - e^{-0.2\cdot 8}) \simeq 0.2019.\]

Del enunciado también podemos deducir la probabilidad de que un cliente tomado al azar sea cliente de cada una de las tiendas. Las únicas proporciones que suman 1 y cumplen que la tercera es la suma de las otras dos, que son iguales, es la siguiente:

\[P(A) = P(B) = 0.25; \; P(C) = 0.5.\]

Entonces ya tenemos todos los datos para calcular la probabilidad del suceso \(D\):

\[P(D) = P(D|A)P(A)+P(D|B)P(B)+P(D|C)P(C) =\\ = 0.0183\cdot 0.25 + 0.1353 \cdot 0.25 + 0.2019 \cdot 0.5 \simeq \boxed{0.1393}.\]

Cuestión 1.b)

En este caso la probabilidad pedida es \(P(A|D)\), que calculamos con la fórmula de Bayes, donde el denominador ya lo hemos calculado:

\[P(A|D) = \frac{P(D|A)P(A)}{P(d)}= \frac{0.0183\cdot 0.25}{0.1393} \simeq \boxed{0.0329}. \]

Cuestión 2.a)

Ahora no estamos mezclando poblaciones, sino sumando variables aleatorias. En concreto, las ventas totales recaudadas por la empresa será una variable aleatoria que resulta de operar con las variables aleatorias \(V_A\), \(V_B\) y \(V_C\)):

\[Y = 25 + V_A + V_B + 0.5\cdot V_C.\]

Por la propiedad aditiva de la distribución normal, al ser variables independientes, esta variable sigue una distribución normal de parámetros:

\[\mu_Y = 25 + 100 + 150 + 0.5\cdot 140= 345,\] \[\sigma_Y = \sqrt{10^2 + 20^2 + 0.5^2\cdot 40^2} = 30,\]

Y por tanto:

\[\boxed{Y \sim N(345, 30)},\]

Cuestión 2.b)

Una vez tenemos la distribución de probabilidad, obtenemos la probabilidad de la manera habitual:

\[P[Y < 300] = P \left[ \frac{Y-\mu_Y}{\sigma_Y} < \frac{300 -345}{30}\right] = \\ P[Z < -1.5] = P[Z > 1.5] \simeq \boxed{0.0668}.\]

Las probabilidades de este ejemplo se resuelven de forma análoga a los anteriores. Se deja como ejercicio para el lector comprobar por sí mismo los resultados ofrecidos a través del programa de su elección.

7.4 Otros modelos de distribución de probabilidad

Los modelos vistos en este capítulo y el anterior cubren la mayoría de los problemas cotidianos de modelización. Existen otros modelos de distribución que se aplican a problemas específicos. Para finalizar este capítulo, se proporciona una breve descripción de las que aparecen en la norma ISO 3534-1.

• Distribución lognormal. Una variable lognormal, al transformarla mediante el logaritmo será una normal.

• La distribución Gamma. Ya se ha comentado que es una generalización de la distribución exponencial, y modeliza el tiempo hasta \(k\) eventos

• La distribución Beta. Es muy útil para modelizar proporciones y probabilidades.

• La distribución de Weibull. También se utiliza para modelizar tiempos de vida, y es muy flexible describir formas muy diferentes de la distribución mediante el ajuste de sus parámetros. Es también una distribución de valores extremos (tipo III). La norma incluye otras dos distribuciones de valores extremos: Tipo I (Gumbel) y Tipo II (Fréchet).

• La distribución normal multivariante. Se aplica a vectores aleatorios donde todas sus componentes son variables aleatorias normales.

• La distribución multinomial. Se aplica a características cualitativas multiclase. Es el equivalente multivariante a la distribución binomial, donde no solamente hay dos resultados posibles sino más de dos. Entonces tenemos un vector aleatorio con tantas componentes como clases posibles (resultados del experimento). Cada componente del vector aleatorio sigue una distribución binomial.

En el apéndice C se puede encontrar un resumen de todas las distribuciones de probabilidad y sus principales características.

7.5 Convergencia de variables aleatorias

7.5.1 Introducción

En este apartado vamos a tratar brevemente la convergencia de variables aleatorias y su aplicación al cálculo de probabilidades. La convergencia tiene también importantes aplicaciones en inferencia estadística que no se tratarán en este libro. Por convergencia se entiende que una determinada familia de distribuciones de probabilidad que dependen de un parámetro \(n \in \mathbb{N}\), a medida que aumenta \(n\) la distribución se asemeja o tiende a otra determinada distribución de probabilidad \(X\)⁷¹.

Una sucesión de variables aleatorias es un conjunto de variables aleatorias:

\[\{ X_n \}: \{X_1, X_2, \ldots, X_n, \ldots \},\] definidas para todo \(n \in \mathbb{N}\) sobre el mismo espacio de probabilidad \((\Omega, \aleph, \wp)\). Asociadas a la sucesión de variables aleatorias tenemos también la sucesión de la imagen del espacio muestral \(\{X_n(\omega)\}\) y la sucesión de las probabilidades del espacio muestral \(\{P_{X_n}(\omega)\}\).

Vamos a considerar tres tipos de convergencia: convergencia en probabilidad, convergencia casi segura y convergencia en ley o en distribución. Una sucesión de variables aleatorias \(\{ X_n \}\) converge en probabilidad a \(X\) y lo representamos por:

\[\{ X_n \} \mathop{\longrightarrow}^{p}X\]

si:

\[\forall \; \epsilon>0, \lim_{n \to \infty} P[|X_n-X|<\epsilon] =1.\] La convergencia casi segura, representada por:

\[\{ X_n \} \mathop{\longrightarrow}^{c.s.}X,\] implica que:

\[\forall \; \epsilon>0, \lim_{n \to \infty} P[\omega \in \Omega : |X_n(\omega)-X(\omega)|<\epsilon] =1.\] Por último, la convergencia en distribución:

\[\{ X_n \} \mathop{\longrightarrow}^d X,\] implica que:

\[\lim_{n \to \infty} F_{X_n} = F_X.\] La relación entre los tres tipos de convergencia es la siguiente:

\[\text{casi segura } \implies \text{ en probabilidad } \implies \text{ en distribución},\]

pero lo contrario no se cumple siempre.

Nótese que podemos interpretar la convergencia casi segura en el ámbito de los sucesos, la convergencia en probabilidad en el ámbito de las variables aleatorias (imagen de los sucesos en los números reales, independientemente de cuáles sean estos) y la convergencia en distribución en el ámbito de las funciones (independientemente de cuáles sean las variables y los sucesos).

7.5.2 Leyes de los grandes números

En este apartado veremos dos resultados importantes como consecuencia de la convergencia de variables aleatorias. Para ello vamos a considerar la sucesión \(\eta_n\) como la media de las \(n\) variables aleatorias de la sucesión \(\{X_n\}\):

\[\eta_n=\frac{X_1 + X_2 + \ldots, X_n}{n}.\]

7.5.2.1 Ley débil de los grandes números

Una sucesión \(\{X_n\}\) de variables aleatorias cumple la Ley débil de los grandes números si la sucesión:

\[\eta_n=\frac{\sum\limits_{i=1}^n (X_i - E[X_i])}{n}\] converge en probabilidad a cero:

\[\eta_n \mathop{\longrightarrow}^p 0.\]

Esto implica que tomando sucesivas muestras, podré acercarme al valor verdadero de la media tanto como quiera aumentando \(n\).

7.5.2.2 Ley fuerte de los grandes números

Una sucesión \(\{X_n\}\) de variables aleatorias cumple la Ley fuerte de los grandes números si la sucesión:

\[\eta_n=\frac{\sum\limits_{i=1}^n (X_i - E[X_i])}{n}\]

converge casi seguro a cero:

\[\eta_n \mathop{\longrightarrow}^{c.s.} 0.\] Esto implica que, en el límite, la media de sucesivas variables aleatorias es el valor real de la media.

7.5.3 Teorema central del límite

Consideremos una sucesión de variables aleatorias \(\{X_n\}, n \in \mathbb{N}\), entonces diremos que esa sucesión cumple el teorema central del límite si y solamente si la suma de las variables menos sus esperanzas, dividida por la raíz cuadrada de la suma de sus varianzas, converge en distribución a una distribución normal estandarizada:

\[\eta_n = \frac{\sum\limits_{i=1}^n (X_i - E[X_i])}{\sqrt{\sum\limits_{i=1}^nV[X_i]}} \mathop{\longrightarrow}^d N(0; 1).\]

Es condición suficiente para que \(\{X_n\}\) cumpla el teorema central del límite que las variables de la sucesión sean independientes e idénticamente distribuidas con media \(\mu=E[X_n]\) y varianza \(\sigma^2=V[X_n]\):

\[\eta_n = \frac{S_n - n\mu}{\sigma\sqrt{n}} \mathop{\longrightarrow}^d N(0; 1),\]

siendo \(S_n\) la serie de variables aleatorias \(S_n=\sum\limits_{i=1}^n X_i\).

7.5.4 Aproximación de distribuciones

El teorema central del límite se aplica directamente a cualquier sucesión de variables aleatorias independientes e idénticamente distribuidas. Un caso particular es la aplicación a la distribución binomial. Efectivamente, la distribución binomial es una suma de distribuciones independientes de Bernoulli con parámetro \(p\), y entonces \(S_n \equiv Bin(n;p)\):

\[\frac{S_n - np}{\sqrt{npq}}\mathop{\longrightarrow}^d N(0;1),\] con \(q=1-p\). La figura 7.14 muestra las funciones de probabilidad de variables aleatorias que se distribuye según un modelo binomial, para distintos valores del parámetro \(n\). Podemos ver cómo a medida que aumenta \(n\), la distribución se aproxima más a la forma de la distribución normal.

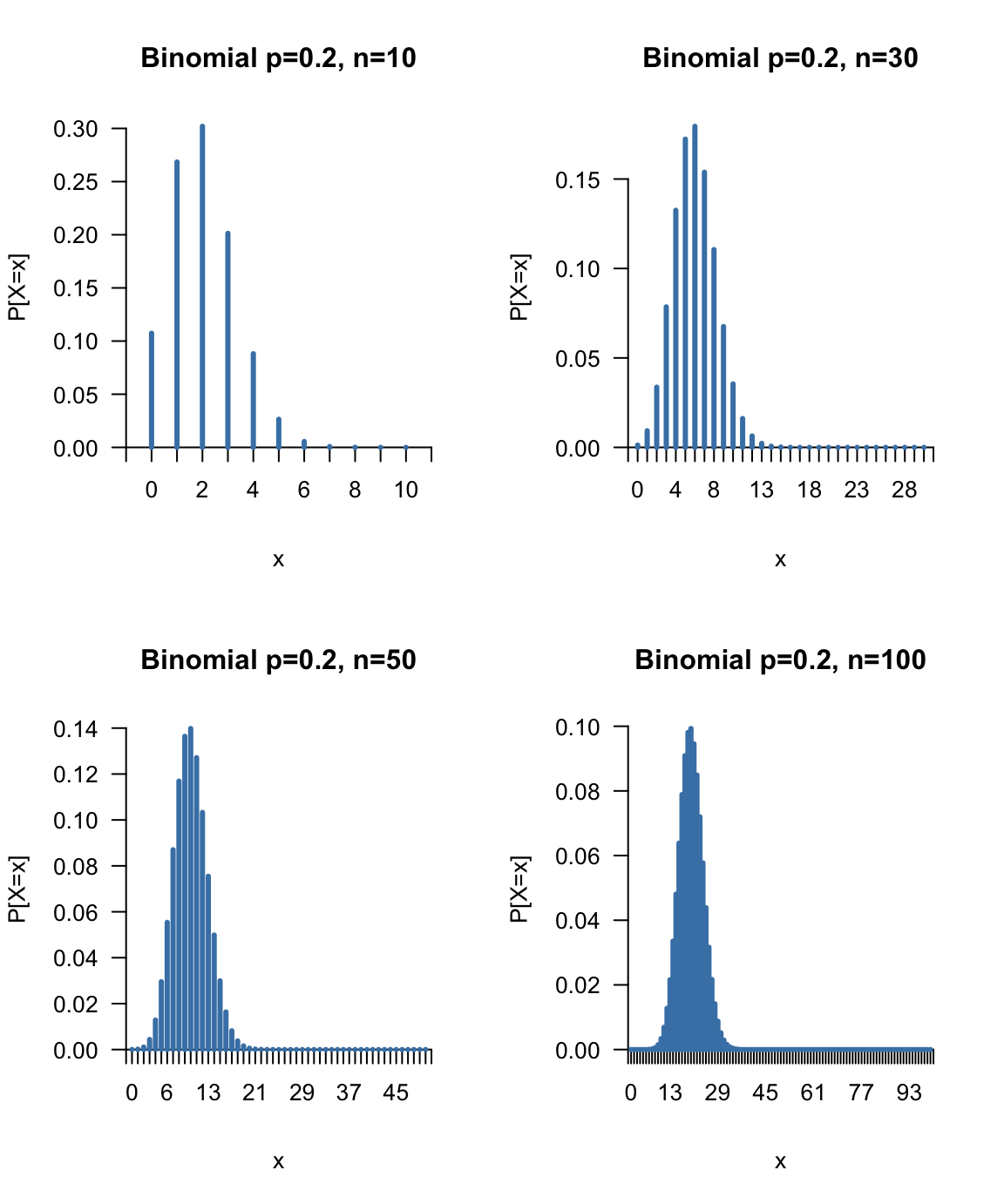
Figura 7.14: El teorema central del límite y la distribución binomial

En la práctica, el teorema central del límite lo vamos a utilizar para aproximar la distribución binomial a la distribución normal para valores grandes de \(n\), en general valores mayores de 100. Tal y como vimos en el capítulo ??, también la podíamos aproximar mediante la distribución de Poisson, con lo que el esquema de aproximaciones quedaría así:

\[\boxed{B(n;p) \begin{cases} \mathop{\longrightarrow}\limits^{p<0.05, np \text{ estable }} \leadsto Pois(np)\\ \mathop{\longrightarrow}\limits^{n\geq 100} \leadsto N(np; \sqrt{npq}) \end{cases}}\]

Del mismo modo, una suma de \(n\) distribuciones de Poisson de parámetro \(\lambda\) se puede aproximar por una distribución normal:

\[\boxed{\sum\limits_{i=1}^n Pois(\lambda)\mathop{\longrightarrow}\limits^{n\geq 100} \leadsto N(n\lambda; \sqrt{n\lambda})}\]

En general, cualquier suma de variables aleatorias independientes e idénticamente distribuidas se podrá aproximar por la distribución normal estandarizada si \(n\) es suficientemente grande.

Una fábrica de medicamentos realiza pruebas clínicas con 300 nuevos fármacos potenciales. Cerca del 20% de las sustancias que alcanzan esta etapa reciben finalmente la aprobación para su venta. ¿Cuál es la probabilidad de que se aprueben al menos 45 de los 300 medicamentos?

Definimos \(X:\) número de medicamentos aprobados, en una serie de 300 experimentos de Bernoulli con probabilidad \(p=0.2\). Entonces:

\[X\sim \mathit{Bin}(300; 0.2).\]

No podemos utilizar la aproximación de Poisson ya que \(p>0.05\), pero sí la de la normal porque \(n\geq100\). Así:

\[X \leadsto N(300\cdot 0.2; \sqrt{300\cdot 0.2 \cdot 0.8}\equiv N(60, \sqrt{48}).\] Ahora tipificamos y calculamos probabilidades de la normal estandarizada:

\[P[X > 45 ]= P\left[\frac{X-60}{\sqrt{48}} >\frac{45-60}{\sqrt{48}}\right]=P[Z>-2.16]=\\ =1-P[Z>2.16]= 1-0.0154=0.9846.\]

7.6 Distribuciones relacionadas con la normal